BCAM Course | Control Theory Made Easy: A Mathematical Perspective  with Application Examples

Course Details: Modality, Schedule, and Venue:

An 18-hour course that will be delivered over 6, 3-hour, sessions. The course will combine theoretical and practical instruction, with the added focus on hands-on exercises and real-world examples. The course will maintain a balanced approach, dedicating 60% of the course to theory and 40% to practical application. The course will take place at the Basque Center for Applied Mathematics (BCAM). Participants can expect to obtain a strong foundation in control engineering, including the ability to analyse and design control systems.

Course Roadmap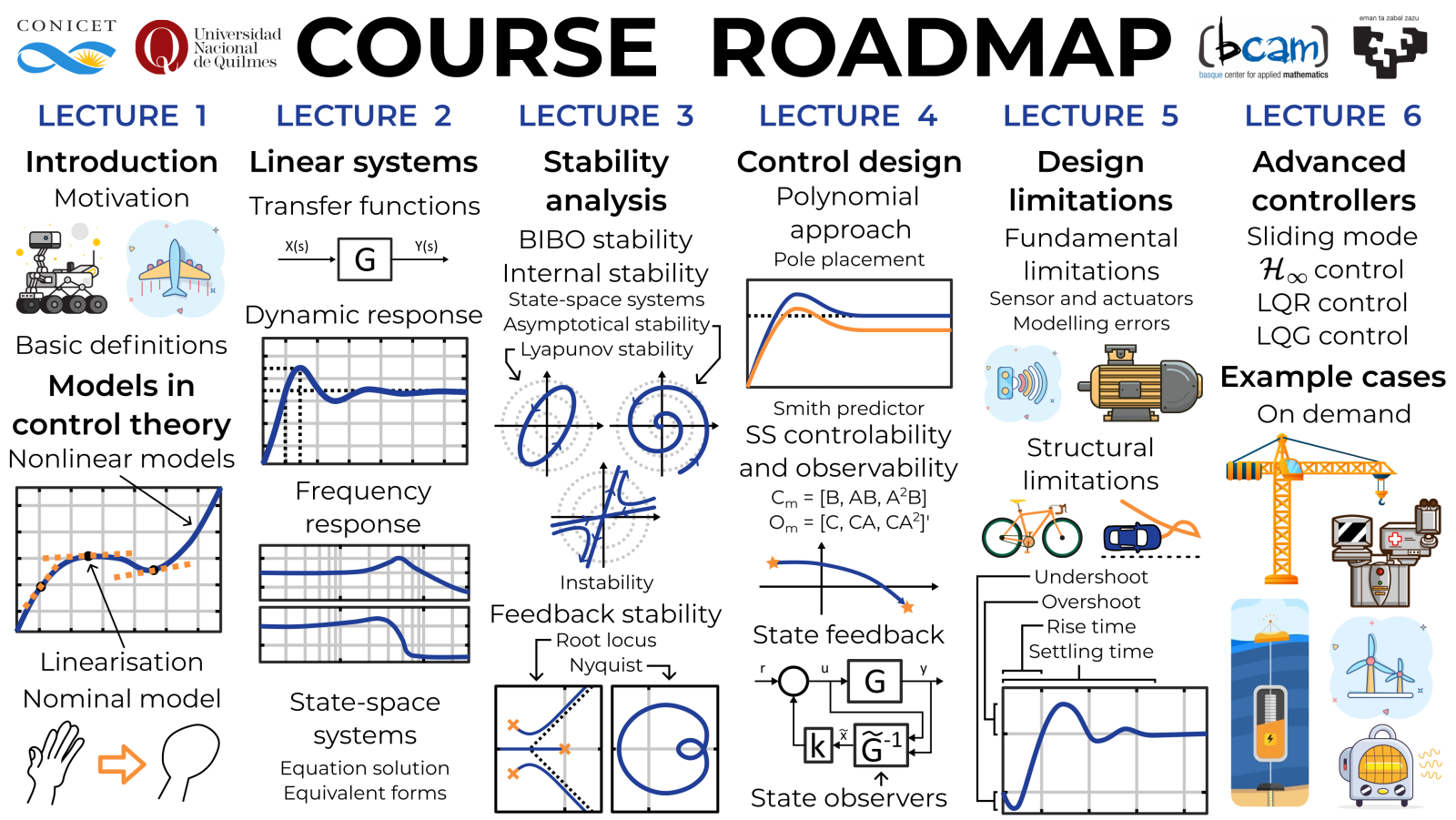


 

• DAY 1: Friday, September 01, 2023 - 10:00 - 13:00

• DAY 2: Tuesday, September 05, 2023 - 14:30 - 17:30 

• DAY 3: Friday, September 08, 2023 - 10:00 - 13:00

• DAY 4: Wednesday, September 13, 2023 - 14:30 - 17:30 

• DAY 5: Thursday, September 14, 2023 - 14:30 - 17:30 

• DAY 6: Tuesday, September 19, 2023 - 14:30 - 17:30

General Objective:

The general objective is to provide the theoretical basis for the treatment of control systems, from a classical and modern perspective (frequency and time domains).

Prerequisite Knowledge:

This course assumes knowledge in linear algebra and familiarity with the Laplace transform. Additionally, a basic understanding of ordinary differential equations is necessary.

Software Requirement:

A simulation and analytical computing software, with dedicated toolboxes for control systems, is necessary. The use of Matlab/Simulink by MathWorks, with the Control System Toolbox, is recommended. Alternatively, other platforms such as GNU Octave or Scilab, along with Sci cosim and Scicos, respectively, or Python, can be considered.

Literature:

Mandatory references:

• Goodwin, G. C., Graebe, S. F., & Salgado, M. F. (2001). Control system design. Prentice Hall.
• Chen, C.-T. (1999). Linear system theory and design (3rd ed.). Oxford University Press.

Additional references:

• Bay, J. S. (1999). Fundamentals of linear state space systems. WCB/McGraw-Hill.
• Kailath, T. (1980). Linear systems. Prentice Hall.
• Kuo, B. C. (1996). Sistemas de control automático (7th ed.). Prentice-Hall Hispanoamericana.
• Rugh, W. J. (1995). Linear system theory (2nd ed.). Prentice Hall.
• Sanchez-Pena, R. S., & Sznaier, M. (1998). Robust systems theory and applications. John Wiley & Sons, Inc.
• Sontag, E. D. (1998). Mathematical control theory: Deterministic finite dimensional systems (2nd ed.). Springer-Verlag.