ML
Machine Learning
Our goal is to develop novel and efficient machine learning algorithms able to deal with new data-related practical problems. We also pursue the mathematical modeling of these algorithms in order to provide theoretical guarantees of their performance.
In the machine learning research line we deal with data problems coming from different scenarios: industry, biosciences, health, economy, etc. We pursue the developments of new machine learning algorithms that can efficiently tackle these problems. Particularly, we consider problems that account for a variety of data types: from time series, to steaming data or images and speech, and a wide range of modelization techniques and mathematical formalisms such as: probabilistic graphical models, Bayesian approaches, deep learning, etc.
The research carried out in the machine learning line is inspired in problems that appear in other scientific, technological or economical disciplines. We develop new machine learning methods and algorithms related with the main data analysis activities such as clustering, supervised classification, feature subset selection, etc. to solve this kind of problems. Based on the specific characteristics of the problem at hand, we design tailored but general algorithms that extract as much information as possible from the available data providing efficient machine learning models that solve the problem.
In addition to that, we also develop mathematical tools able to model the behavior and performance of the algorithms: studying their convergence, the estimation of the performance, the behavior of the algorithms in terms of computational time and memory requirements, etc.
During the last years the machine learning line has worked with different machine learning problems and algorithms. Particularly, we can emphasize the work done in the area of time series mining and data streaming, the adaptation of classical clustering algorithms such as k-means or k-medoids to massive data environments, the probabilistic modeling of permutations and ranked data or the developments in anomaly detection, and the analysis of crowd learning environments.
In terms of formalisms, we strongly rely on probabilistic modeling, using different tools and techniques such as probabilistic graphical models and Gaussian process to name, which in most cases are learned under a Bayesian perspective. We also pursue the use of deep learning when we consider it the most appropriate technique for the problem at hand.
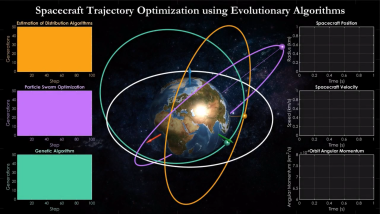
Hierarchical sequence optimization for spacecraft transfer trajectories based on the employment of meta-heuristics
Description: This video shows the simulation of hierarchical sequence optimization for spacecraft transfer trajectories based on the employment of meta-heuristics. Three types of evolutionary algorithms including ìGenetic Algorithmî, ìParticle Swarm Optimizationî and ìEstimation of Distribution Algorithmsî are used in optimal guidance approach utilizing low-thrust trajectories. Different initial orbits are considered for each algorithm while the orbits are expected to have the same shape and orientation at the end of space mission.
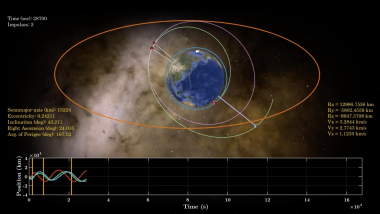
Multi-impulse Long-Range Space Rendezvous via Evolutionary Discretized Lambert Approach
Transfering satellites between space orbits is a challenging task. Due to the complexity of the space systems, finding optimal transfer trajectories requires efficient approaches. This video shows the simulation of the satellite motion in a space mission, where a new evolutionary algorithm is developed and utilized for the orbit transfer. The satellite performs multiple transfers between intermediate orbits until it reaches the desired destination. Novel heuristic mechanisms are used in the development of the optimization algorithm for spacecraft trajectory design. Simulation results indicate the effectiveness of the algorithm in finding optimal transfer trajectories for the satellite.
Efficient Meta-Heuristics for Spacecraft Trajectory Optimization
Algorithms for large orienteering problems
Advances on time series analysis using elastic measures of similarity
K-means for massive data
Theoretical and Methodological Advances in semi-supervised learning and the class-imbalance problem
KmeansLandscape
Study the k-means problem from a local optimization perspective
Authors: Aritz Pérez
License: free and open source software
Placement
Local
PGM
Procedures for learning probabilistic graphical models
Authors: Aritz Pérez
License: free and open source software
Placement
Local
On-line Elastic Similarity Measures
Adaptation of the most frequantly used elastic similarity measures: Dynamic Time Warping (DTW), Edit Distance (Edit), Edit Distance for Real Sequences (EDR) and Edit Distance with Real Penalty (ERP) to on-line setting.
Authors: Izaskun Oregi, Aritz Perez, Javier Del Ser, Jose A. Lozano
License: free and open source software
Probabilistic load forecasting based on adaptive online learning
This repository contains code for the paper Probabilistic Load Forecasting based on Adaptive Online Learning
Authors: Veronica Alvarez
License: free and open source software
MRCpy: a library for Minimax Risk Classifiers
MRCpy library implements minimax risk classifiers (MRCs) that are based on robust risk minimization and can utilize 0-1-loss.
Authors: Kartheek Reddy, Claudia Guerrero, Aritz Perez, Santiago Mazuelas
License: free and open source software
Minimax Classification under Concept Drift with Multidimensional Adaptation and Performance Guarantees (AMRC)
The proposed AMRCs account for multivariate and high-order time changes, provide performance guarantees at specific time instants, and efficiently update classification rules.
Authors: Veronica Alvarez
License: free and open source software
Efficient learning algorithm for Minimax Risk Classifiers (MRCs) in high dimensions
This repository provides efficient learning algorithm for Minimax Risk Classifiers (MRCs) in high dimensions. The presented algorithm utilizes the constraint generation approach for the MRC linear program.
Authors: Kartheek Reddy
License: free and open source software
efficient learning algorithm for Minimax Risk Classifiers (MRCs) in high dimensions
This repository provides efficient learning algorithm for Minimax Risk Classifiers (MRCs) in covariate shift framework.
Authors: Jose Segovia
License: free and open source software
BayesianTree
Approximating probability distributions with mixtures of decomposable models
Authors: Aritz Pérez
License: free and open source software
Placement
Local
MixtureDecModels
Learning mixture of decomposable models with hidden variables
Authors: Aritz Pérez
License: free and open source software
Placement
Local
FractalTree
Implementation of the procedures presented in A. Pérez, I. Inza and J.A. Lozano (2016). Efficient approximation of probability distributions with k-order decomposable models. International Journal of Approximate Reasoning 74, 58-87.
Authors: Aritz Pérez
License: free and open source software
Minimax Forward and Backward Learning of Evolving Tasks with Performance Guarantees
This repository is the official implementation of Minimax Forward and Backward Learning of Evolving Tasks with Performance Guarantees.
Authors: Veronica Alvarez
License: free and open source software