WAVE
Linear and Non-Linear Waves
We propose new challenges and develop original analytical tools to entail significant progress on three different aspects of some fundamental Partial Differential Equations of Mathematical Physics:
- Talbot Effect and turbulence
- Confinement properties of Non-relativistic Hamiltonians
- Uncertainty Principles and Applications
What these three topics have in common is that they will be studied making a modern use of classical techniques of Harmonic Analysis, such as: Oscillatory Integrals and Gauss Sums to describe the dynamics of vortex filaments, Singular Integral Operators like the Cauchy Integral to study shell interactions for Dirac equations and confinement, and Carleman estimates to obtain lower bounds that eventually lead to prove new uncertainty principles. More concretely,
- We study the evolution of vortex filaments with corners. The dynamics is mainly self-similar as for example the one exhibited by the vortex loops created by the smoke from a cigarette or by the symmetrical pair of vortices generated behind a triangular wing. Corners seem to appear naturally in the process of reconnection of a counterrotating vortex pair.
- We want to develope a general theory to treat singular electromagnetic Hamiltonians for Dirac and Schrödinger equations with a special attention to the so called delta-shell interactions.
- We study Hardy’s uncertainty principle for the discrete Laplacian by following the connection between some classical uncertainty principles and uniqueness properties of dispersive and parabolic PDE’s.
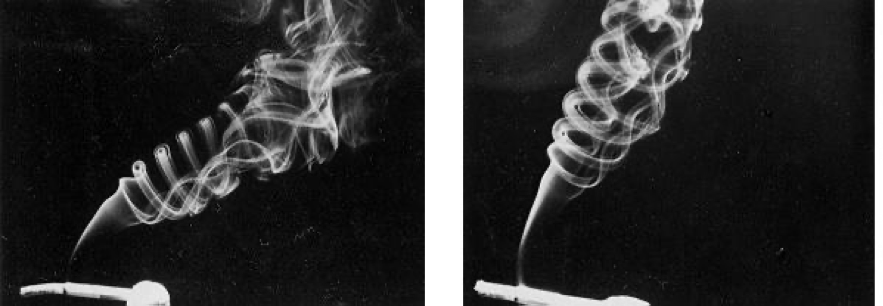
Vortex loops created by the smoke from a cigarette
Pair of vortices generated behind a triangular wing
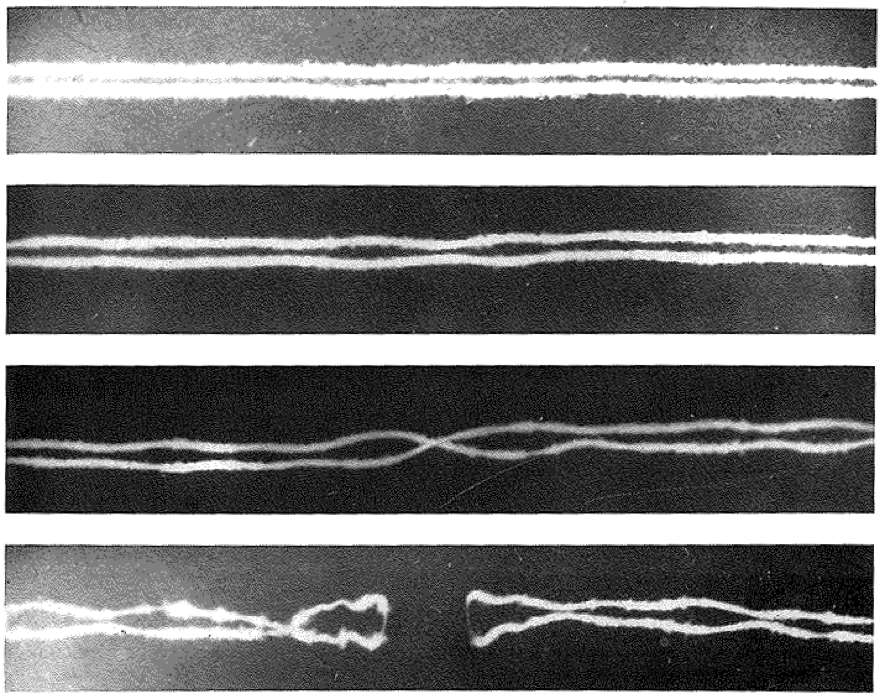
Reconnection of a counterrotating vortex pair
- We want to establish the so-called Frisch-Parisi conjecture for the evolution of regular polygons within the framework of the Vortex Filament Equation. This conjecture, initially proposed in the setting of fully developed turbulence, is the first time that would be established in a non-linear model that moreover, is directly related to Fluid Mechanics.
VFE is a geometric non-linear PDE that originated as a simple model for the evolution of vortex filaments and captures, at the qualitative level, relevant features of the real dynamics. For example, this model predicts, thanks to the results obtained by V. Banica, F. De la Hoz, and Luis Vega the axis-switching phenomena that has been observed in non-circular jets with nozzles that have the shape of a regular polygon. The model also predicts the creation of polygonal structures with an arbitrary number of sides depending on the precise value of Gauss sums, suggesting that the different corners behave like different vortex filaments that interact with each other in such a way that the dynamics seem chaotic. This is a geometric version of well known Talbot effect of Optics. This geometric point of view has had important consequences in classical problems in Analysis as those related to the so called Riemann's non differentible function. Results in this direction have been obtained by D. Eceizabarrena and S. Kumar in their PhD thesis. Also the close connection between the Talbot and the Schrödinger evolutions has been positively exploited by D. Eceizabarrena and R. Lucá to address the fractal properties of the sets of uniqueness for the free Schrödinger equation. - The team made by N. Arrizabalaga, A. Mas and L. Vega together with T. Sanz-Perela and B. Benhellal aim to prove that among all the regular and bounded surfaces with a suitable chosen constraint the sphere is the optimal shell from a spectral point of view. This needs to be considered a first and critical step in the resolution of the long standing optimization problem for the so-called MIT bag model for quark confinement.
- Our approach differs completely from the work that has been carried out up to now and is based on methods of PDEs. As a consequence we establish some unknown uniqueness results for dispersive, parabolic and elliptic equations. This work builds up on the collaboration of C.E. Kenig, L. Escauriaza, G.Ponce and L. Vega and also some recent work by A. Fernandez-Bertolin and M. Agirre.
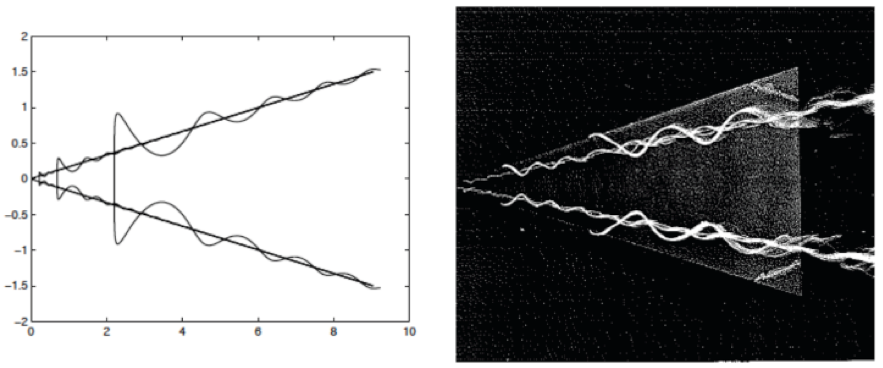
Selfsimilar solutions versus vortices behind a triangular wind
Curlicue in the unit sphere generated at an irrational time
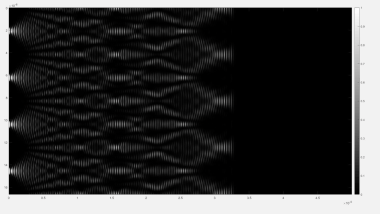
Estudio numérico de la evolución temporal del efecto Talbot para una rejilla de difracción periódica infinita
Este vídeo muestra la propagación de la intensidad de una onda plana tras atravesar una rejilla de difracción infinita y periódica. La simulación se realiza utilizando un método de elementos finitos. Su objetivo es mostrar la evolución temporal y la formación del efecto Talbot.
