AA
Applied Analysis
The Applied Analysis line studies systems of partial differential equations arising in various physically relevant models, with the tools of rigorous theoretical analysis, complemented as needed by numerical simulations.
Current research is concerned with the analytical study of physically motivated systems of PDEs. So far it has concentrated on several major directions:
- The Q-tensor theory describing liquid crystals
- The Smoluchowski-Doi models describing complex non-Newtonian fluids
- Aspects of classical Newtonian fluids
- Elliptic systems of phase transition type
- Simulations of solutions of PDEs using neural networks
- Fluid models encoding heterogeneities: density and temperature variations, presence of magnetic field, non-homogeneous boundary data…
- Description of the dynamics of geophysical flows
- Study of models from turbulence theory
- Analysis of multi-scale processes via singular limits.
- Fluid-structure Interactions: Modelling and mathematical analysis of FSI problems, Existence, uniqueness, singular limits and long time behaviour of the solutions.
- Control of PDE : Controllability, Stabilizability and Optimal control problem for Fluids and Fluid-Structure interaction models.
The models considered by the AA team revolve around (but not limited to) three main themes:
- Mathematical aspects of Materials Science
- Fluid-structure interaction
- Geophysical flows.
Mathematical aspects of Materials Science
One of the main focuses in this direction has been the study of mathematical theories for liquid crystals. The Q-tensor theory and the Smoluchowski-Doi models are relatively new theories, from both a physical and a mathematical point of view. They were proposed in the 70s (the Q-tensor theory), respectively in the 80s (the Smoluchowski-Doi models). They are very popular in the physics community, and in particular Pierre Gilles de Gennes, who proposed the Q-tensor theory, was awarded a Nobel Prize in Physics in 1991 for his work on liquid crystals. Nevertheless they have relatively little mathematical history behind them, most mathematical progress being done in the last decade.

A recent interest is in the Mathematical Design of New Materials theme, which has been the focus of an event co-organised and attended by members of the group at the Isaac Newton Institute, in Cambridge, United Kingdom ( see The mathematical design of new materials - Isaac Newton Institute ). A related programme on the Mathematics for Complex materials was organized at the Hausdorff Institute in Germany (see https://www.mathematics.uni-bonn.de/him/programs/past/tp_2023_01).
The newly created Severo Ochoa Joint Laboratory with the University of Warwick aims to create an international cluster around Mathematical Material Science. The core objectives of this strategic partnership with the ERC/UKRI project CONCENTRATE, are the development of new models for materials science and their analysis.
FLUID-STRUCTURE INTERACTION
The research in this direction is centered on the mathematical analysis of fluid–structure interaction (FSI) and the partial differential equations governing coupled fluid and structural motion. These problems arise naturally in many physical situations and pose challenging questions related to stability, regularity, collision, and long-time behavior. A significant part of the activity has focused on systems in which a rigid body moves inside a viscous or compressible fluid, a framework that models underwater navigation, flight dynamics, and biological swimming.
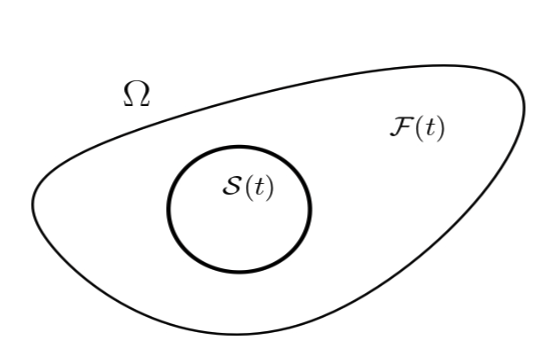
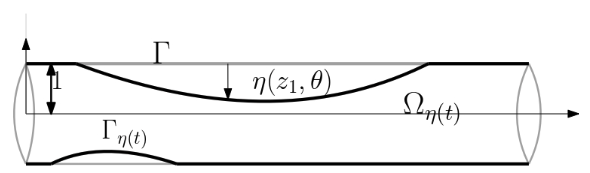
Another major direction involves FSI models for blood flow, where viscous fluids interact with deformable arterial walls, leading to free-boundary PDE–ODE systems. These models are central to understanding hemodynamics in large arteries, yet their mathematical analysis has only advanced significantly in the last decade. Complementary to this, there has been substantial interest in the control and stabilization of both fluid and fluid–structure models, motivated by applications in flow regulation and engineered systems.
Additional work addresses the dynamics of small rigid bodies immersed in fluids, where the influence of the body’s size on the flow becomes subtle, as well as the collision problem in FSI, examining how boundary roughness, body geometry, and physical conditions determine whether impact can occur.
GEOPHYSICAL FLOWS
Geophysical flows are large scale flows, such as currents in the atmosphere or in the ocean. Their dynamics is complex, since it is determined by several competing and interacting factors. The primary ones are the Coriolis force (due to the rotation of the Earth) and the gravity. In addition, variations of density, temperature, salinity (in the case of ocean dynamics) also play a crucial role. Topography (in oceans) and orography (for atmospheric flows) effects are also very important.
The Applied Analysis team studies these questions from the theoretical point of view, adopting a rigorous mathematical approach, with the main goal of improving the knowledge and understanding of those complex phenomena.
Two main approaches are pursued:
- the study of the well-posedness of fluid models presenting heterogeneities in a low regularity framework;
- the asymptotic analysis, via singular limits, of the systems in specific physically relevant regimes, in order to identify correct reduced (i.e. simplified) models, which are easier for theoretical analysis and numerical implementation.
