HA
Harmonic Analysis
This research line deals with various aspects of harmonic analysis and its interaction with other areas.
Harmonic analysis is a rich and dynamic subject that plays a fundamental role within the mathematical sciences. It traces its origins back to Fourier’s celebrated observations on the decomposition of signals into superpositions of simpler waves.
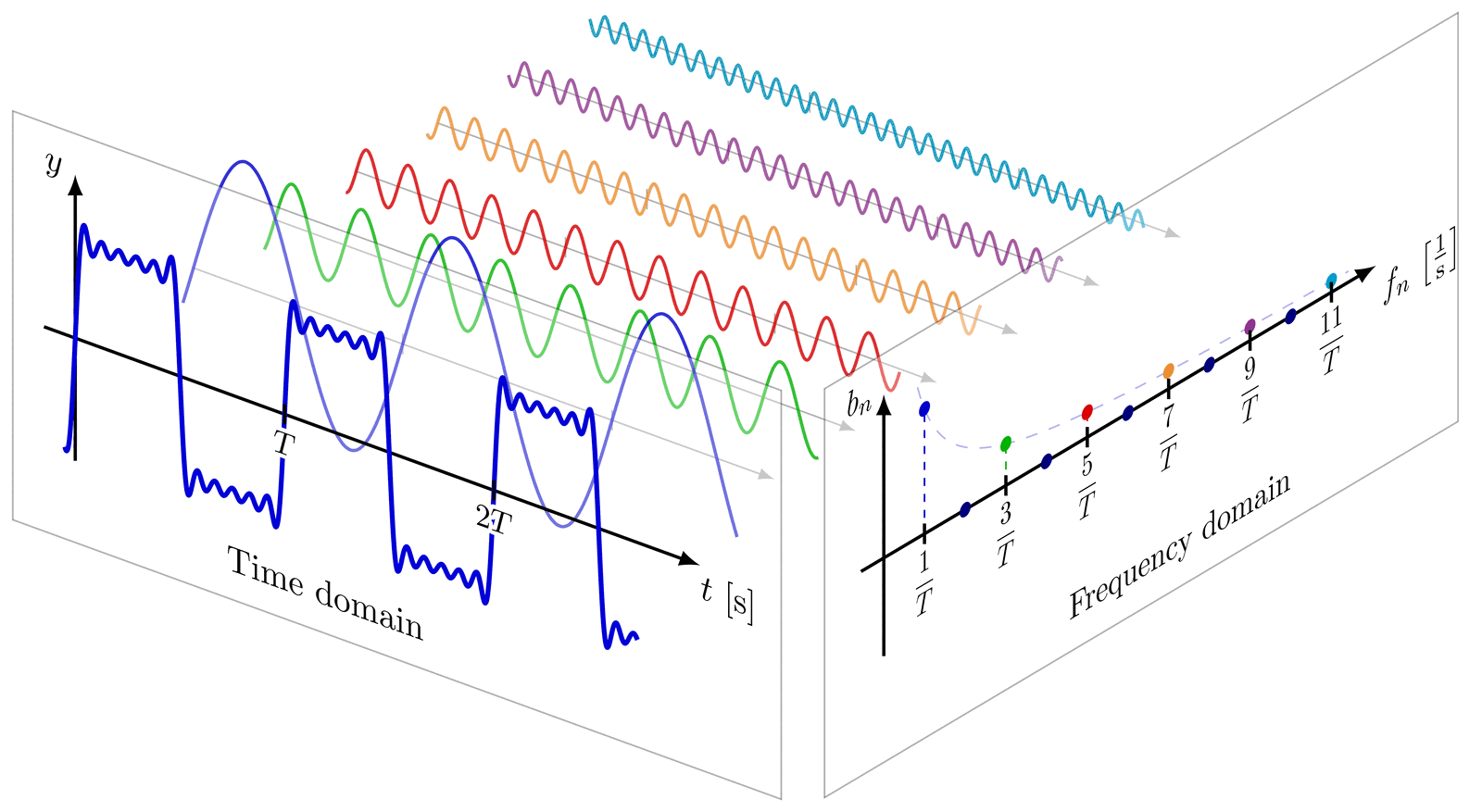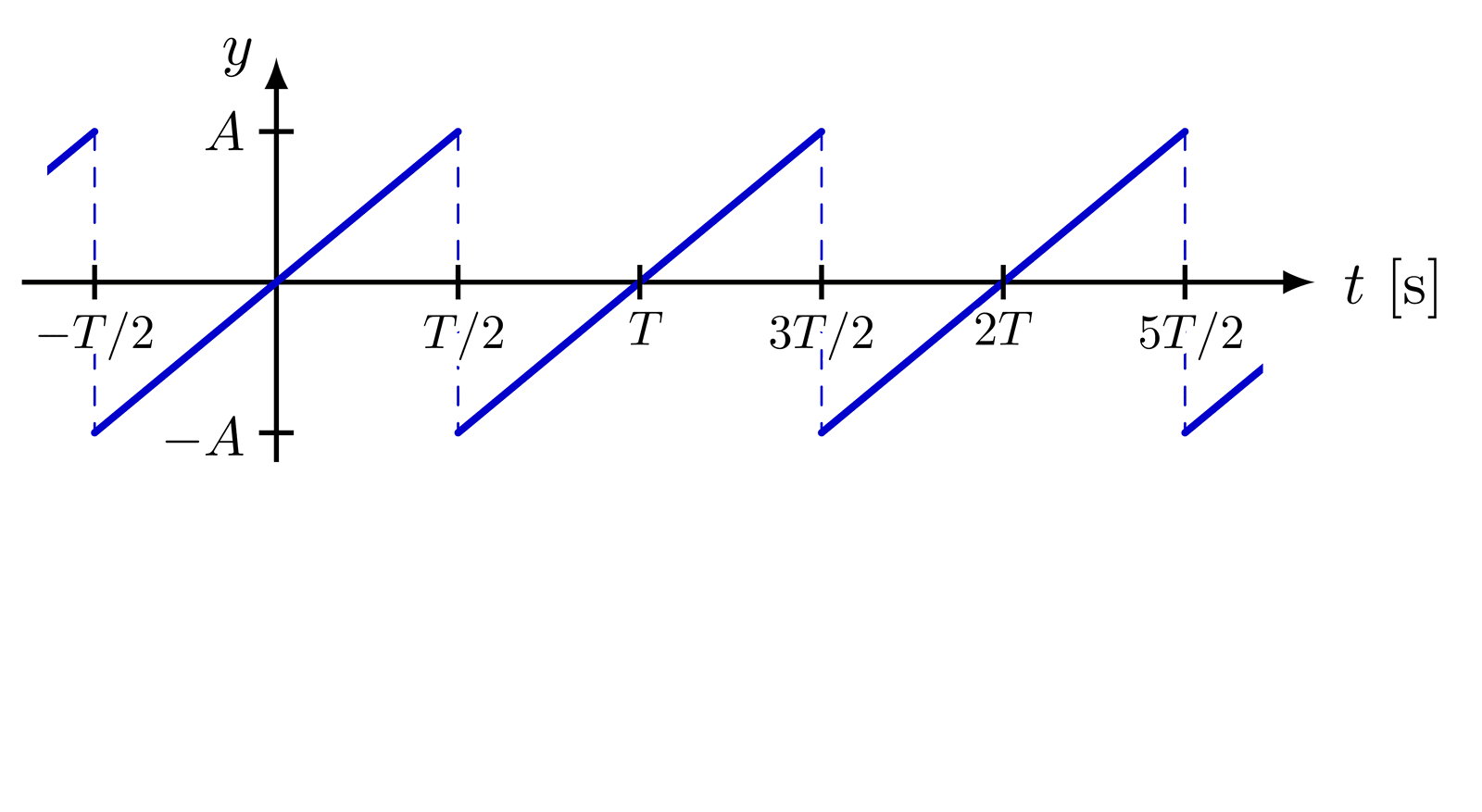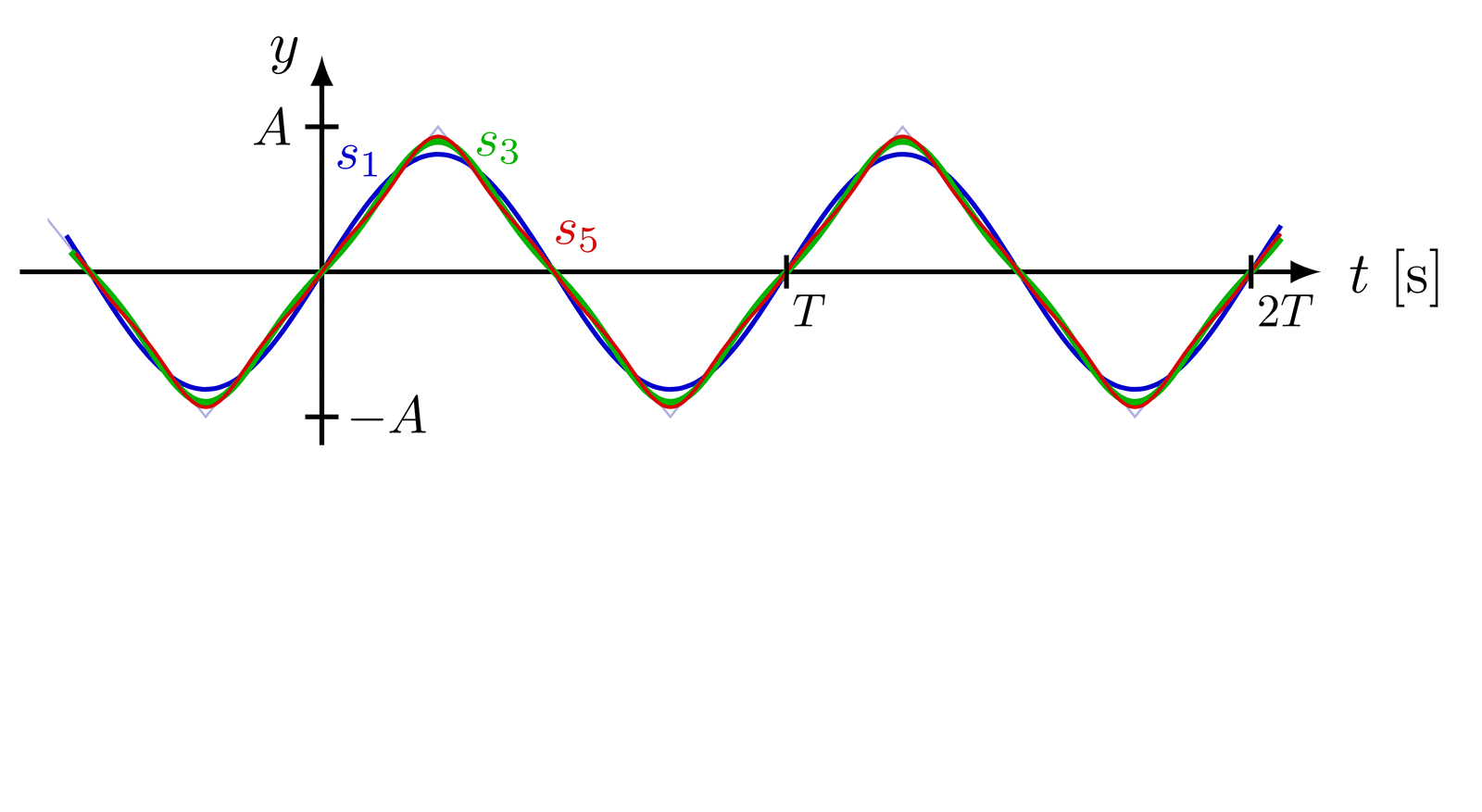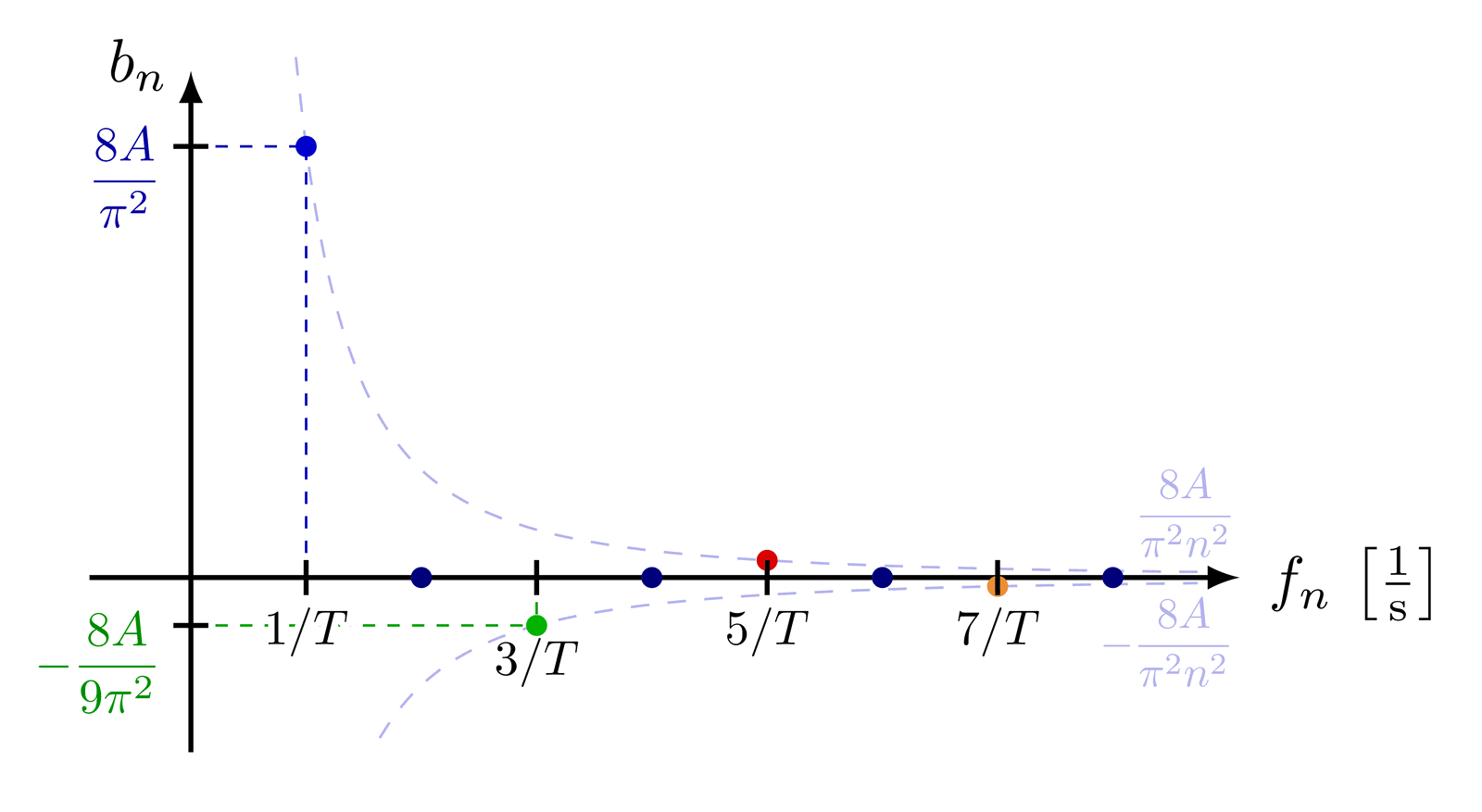
Fourier series representation of different periodic signals (Original by Tikz.net)
Nowadays, the area is concerned with oscillatory phenomena in a much broader sense, and at BCAM we study qualitative and quantitative properties of objects that govern such phenomena. We address a wide range of challenging problems by employing advanced techniques of harmonic analysis, including oscillatory integrals, bilinear restriction estimates, decoupling estimates, singular integrals, Carleman estimates, and multiscale analysis.
The research line is concerned with both classical and modern aspects of harmonic analysis, particularly problems within the field and at its interface with other disciplines, including partial differential equations, spectral theory and number theory. Topics of our interests include:
1. Optimization problems arising from imposing constraints in the Fourier transform of functions and their applications to other areas.
2. Representation of functions via Fourier interpolation formulas and the underlying uncertainty principles.
3. Unique continuation principles in both continuous and discrete settings, and their connections to the Anderson localization phenomenon.
4. Hardy and Hardy-type inequalities, their relation to solutions of the extension problem, and connections with eigenfunctions of Laplace–Beltrami operators.
5. Applications of Fourier restriction theory and local smoothing estimates to the study of the regularity of maximal functions associated with families of dilations of hypersurfaces.
6. Weighted inequalities in harmonic analysis and its applications to the study of Poincaré-Sobolev and isoperimetric inequalities related to the regularity theory of elliptic PDEs.
Topics in Harmonic Analysis; Commutators and directional singular Integrals