MSLMS
Modelling and Simulation in Life and Materials Sciences
Our goal is to enable efficient modelling and detailed simulations of complex systems and problems arising in industry, biology, environment, and society. We put into practice our mathematical expertise in modelling, numerical solution of (integro-) differential equations, enhanced sampling, optimization and parallel computing to devise reliable numerical methodologies and predictive modelling tools (deterministic and probabilistic) for effective and accurate description of a wide range of phenomena in materials and life sciences. Focus is also on application of High Performance Computing (HPC) to problems currently beyond the capacity of existing methods.
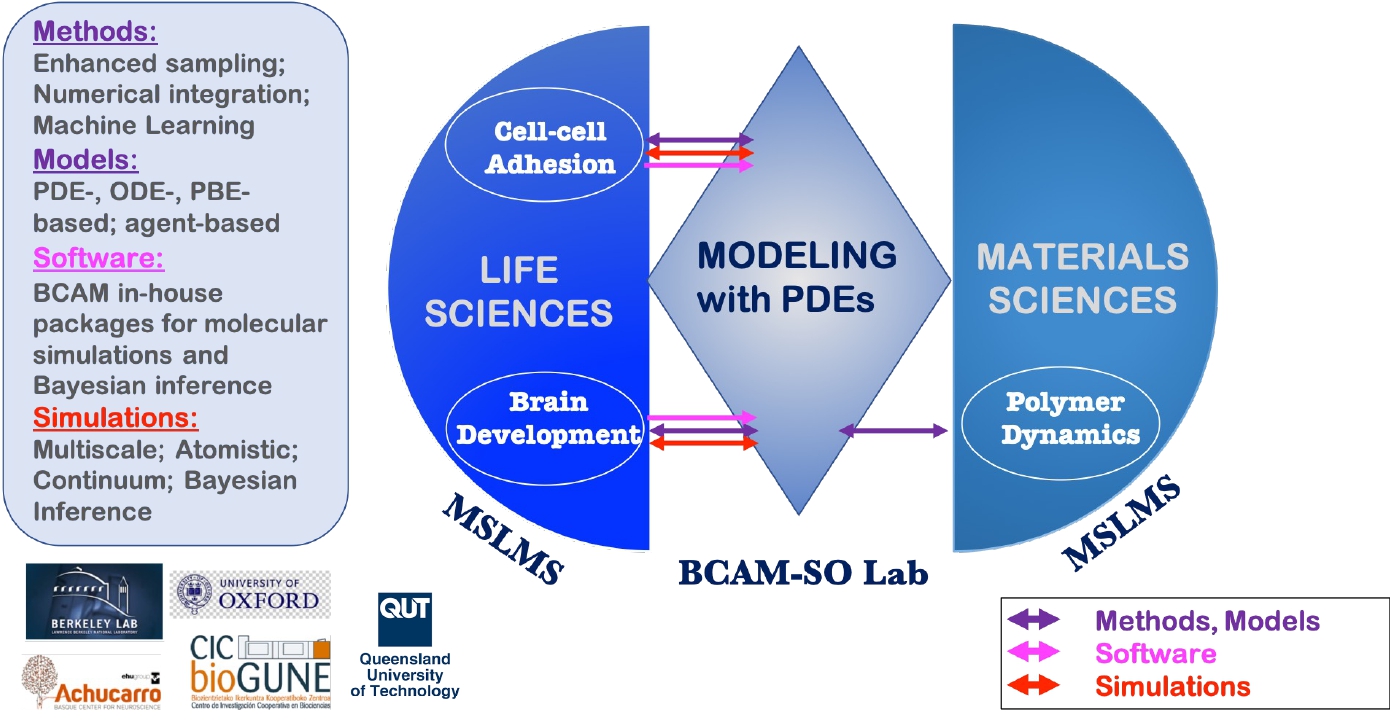
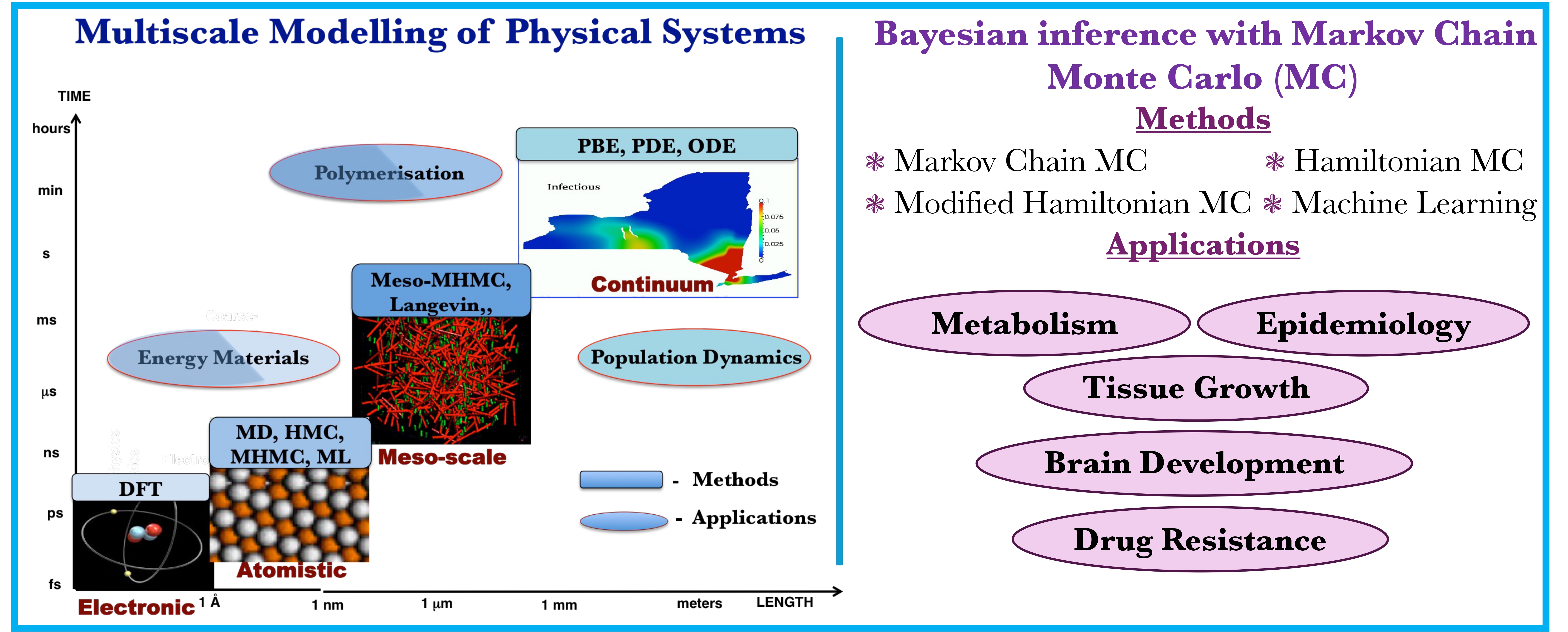
Created in September 2010 and led by Ikerbasque Research Professor E. Akhmatskaya, the MSLMS group was strengthened in 2020 by the joint Oxford - BCAM Severo Ochoa Strategic Lab on Modelling with PDEs in Mathematical Biology coordinated by Prof. J. A. Carrillo (University of Oxford, UK) and Prof. E. Akhmatskaya (BCAM). The research of the group and Lab is complementary (Figure 1).
Activities
MSLMS research activities include
- Modelling of complex multiscale systems covering a wide range of phenomena,
- Numerical algorithms development to efficiently and accurately reproduce the properties of deterministic and stochastic computational models,
- Implementation of our algorithms in open-source software and computational kits, specifically adapted to highly parallelized infrastructures.
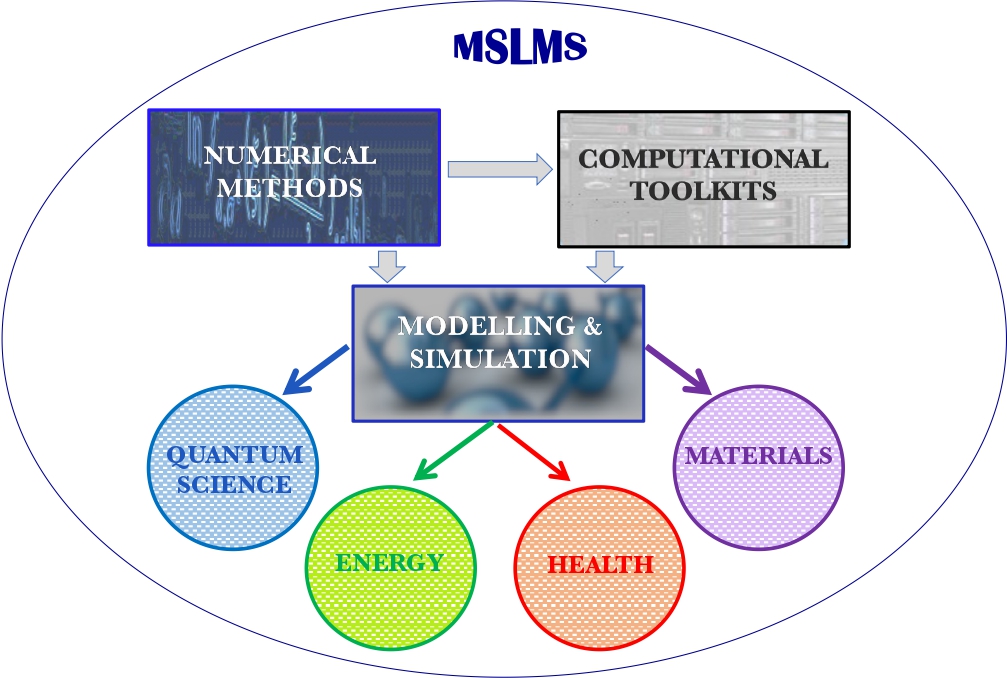
Multidisciplinary research and multitasking are two of the defining features of the MSLMS group. Our work is directed especially, though not exclusively, towards devising and deploying reliable predictive tools in the fields of Quantum Science, Energy, Health and Materials Science (Figure 2).
Methods and Dissemination
The methods developed by the MSLMS group (some of them are patented) aim to overcome the deficiencies of conventional techniques. We also focus on further improvement of their efficiency through developing novel adaptive schemes, numerical integrators and parallel algorithms. We disseminate the developed methodologies to a broad community of scientists and practitioners via open in-house software codes and computational toolkits co-developed in collaboration with our external partners. Besides, we contribute to modernisation of well-established open source highly parallelized software packages.
Fields of Interest
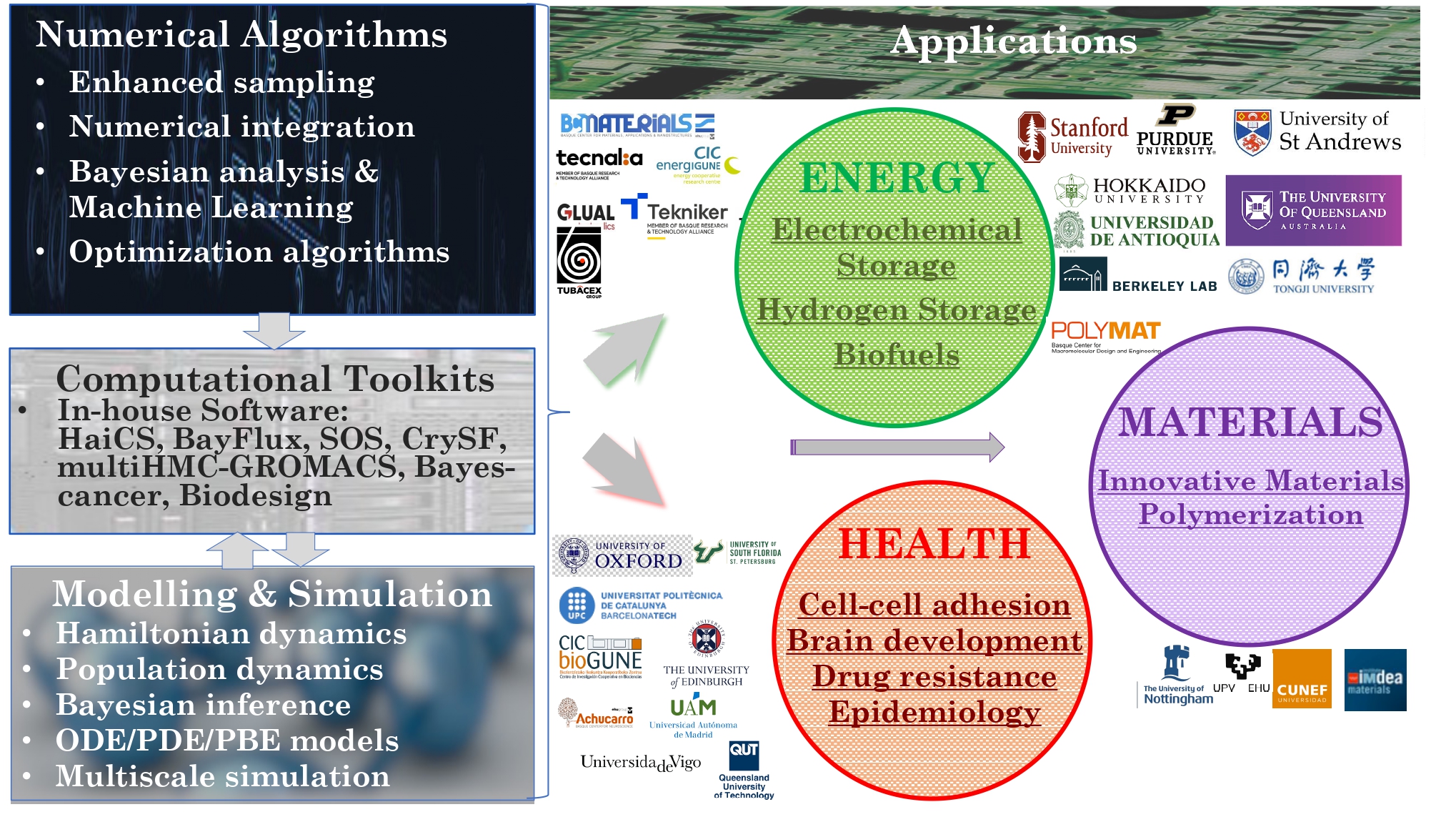
Our researchers employ the most efficient multiscale simulation techniques (in-house or external) and Bayesian inference to answer the important practical questions arising in industry, environment, health and society.
We are most interested in addressing critical societal needs, spanning sustainable energy generation and storage, strategies to combat drug resistance through genomic data mining, foundational advances in quantum modelling and measurement, and the discovery of novel materials for cutting-edge manufacturing technologies (Figures 3 and 4).

Numerical Methods & Algorithms
Advanced numerical methods and algorithms can help applied scientists speed up simulations, improve their reliability and use most efficiently available High Performance computing resources
Stochastic and deterministic enhanced sampling algorithms
One of the computational grand challenges is the development of methodologies for efficient and accurate sampling of high-dimensional spaces. If met, significant progress will be made in understanding many important phenomena in life and physical sciences.
Development of novel efficient Hamiltonian Monte Carlo (HMC) and Modified Hamiltonian Monte Carlo (MHMC) methods, which combine stochastic Markov Chain Monte Carlo (MCMC) with deterministic Hamiltonian Dynamics, is one of our long-standing research interests. Our first methods [1, 2] of these two classes, patented in the US and GB, have clearly demonstrated their superiority in sampling performance over traditional sampling techniques, such as conventional MCMC, molecular dynamics (MD), Hybrid/Hamiltonian Monte Carlo. Today we work on adapting our methods to various simulation scales and statistical ensembles to bridge the time, space and precision scale gaps between simulations and the phenomena of interest. The resulting methods - canonical, constant-pressure, grand-canonical, meso- and multiple-time-stepping variants of HMC and MHMC [2 - 4], as well as the Mix & Match HMC [5], developed specifically for Bayesian inference aim at a wide range of applications.
In addition, we re-design original Monte Carlo algorithms to address particular challenges in applications of interest, e.g. polymerization reactions with delays, quantum measurements, population dynamics, metabolic modelling [6-9].
We also continue to improve performance of the developed samplers by introducing novel adaptive schemes, numerical integrators and parallel algorithms.
Numerical Integration
It often happens that differential equations, widely used in applied mathematics to describe various phenomena, do not have solutions expressible in closed form, and require numerical methods for finding approximate solutions.
Construction of robust and computationally efficient problem-specific integration schemes is, therefore, an important step in facilitating progress in fields as diverse as Classical and Quantum Mechanics, Materials Science, Biology or Engineering.
Common threads of topics we address are geometric integration and splitting algorithms.
Our objectives are to further theoretical knowledge on splitting integrators and other geometric methods, to construct new schemes and apply them to a number of fields. With that in mind, we develop new adaptive multi-stage splitting methods for molecular dynamics and (modified) Hamiltonian/Hybrid Monte Carlo sampling in molecular simulations [10-11] and computational statistics [12], and also devise splitting schemes for solving Population Balance Equations (PBE) [13].
Combined with novel sampling techniques and computational models being introduced by the group, the integrators will make possible accurate modelling of very large complex systems of varied nature [14-16]. Currently, many such systems are beyond the capabilities of the existing modelling approaches.
Machine-learning and data-driven approaches
We incorporate in our modelling methodologies various machine-learning-driven algorithms, to enable large-scale high-resolution simulation in energy and health applications. Bayesian and frequentist machine learning methods assist in performing global optimizations of molecular structures, and help train atomistic force fields in simulation of energy materials. Machine learning algorithms also find their use in tuning performance and accuracy of the sampling techniques, applied for predictive modelling of microbiome and human metabolism, as well as in the analysis of clinical and RNA-Seq data for cancer research [17].
We have also explored the development of data-mining methodologies for the unsupervised analysis of atomistic trajectories. In particular, our recent density-based CrySF method [18] enables the automated characterization of structure and diffusion from the simulation of ordered and disordered solids. The method and its implementation are both robust and versatile, requiring few tuning parameters, and is applicable across a wide range of materials.
Metaheuristic schemes for structural optimization
Atomistic simulations have substantially advanced our understanding of structure–performance relationships in materials science. Yet even small variations in the initial atomic distribution can lead to pronounced differences in the predicted properties. This challenge becomes particularly severe in systems with a combinatorially large configuration space, where exhaustive sampling of all possible states is practically unattainable. The resulting combinatorial explosion (often termed the “exponential wall”) restricts the effectiveness of conventional methods, especially for systems featuring high chemical or structural complexity.
To overcome these limitations, we introduce a novel algorithm designed for efficient exploration of configuration space, leveraging customizable classical energy models in combination with metaheuristic optimization strategies. Implemented within the Search for Optimal Structure (SOS) code, our algorithm balances speed and accuracy while remaining lightweight and straightforward to integrate into existing workflows. It is fully compatible with any metaheuristic solver and accommodates a broad spectrum of energy models, ranging from simple electrostatic interactions to more sophisticated pairwise potentials.
Computational Toolkits
Accurate prediction of complex physical and social processes is often impossible without full utilisation of the capabilities of modern HPC
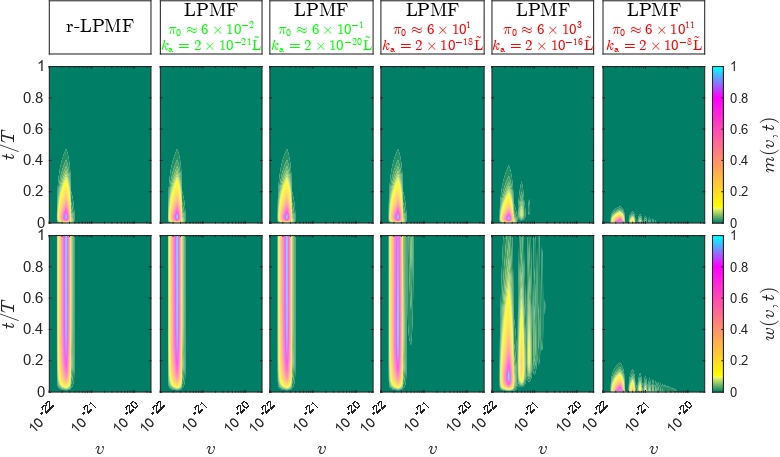
The methodologies derived in MSLMS are implemented in the in-house or well-established open-source software packages. MSLMS in-house computer codes include MultiHMC-GROMACS [4, 10, 11] (Figure 5) - enhanced sampling molecular dynamics and Hybrid Monte Carlo methods in GROMACS package; CrySF [18] (Figure 6 ) - postprocessing analysis of molecular dynamics trajectories; SOS (Figure 7) - efficient structural optimization of solid-state systems with a large number of possible configurations; HaiCS [5, 12] (Figure 8) - statistical sampling and parameter estimation through Bayesian inference using Hamiltonian Monte Carlo methods; CRadPol [19] - simulation of controlled radical polymerization using experimental observations; Ddpm [20] - simulation of dynamic development of particles morphology; complex angular momenta (CAM) analysis suite (PADE II [21], ICS_Regge [22], DCS_Regge [23]); Bayes-cancer [17] - analysis of integrated cell-patient data.
Together with our collaborators from Lawrence Berkeley National Laboratory (USA) we contributed to the development of BayFlux [9] - quantitative metabolic modelling and Biodesign (iGR1773) [25] - biosystems design for production of biofuels.
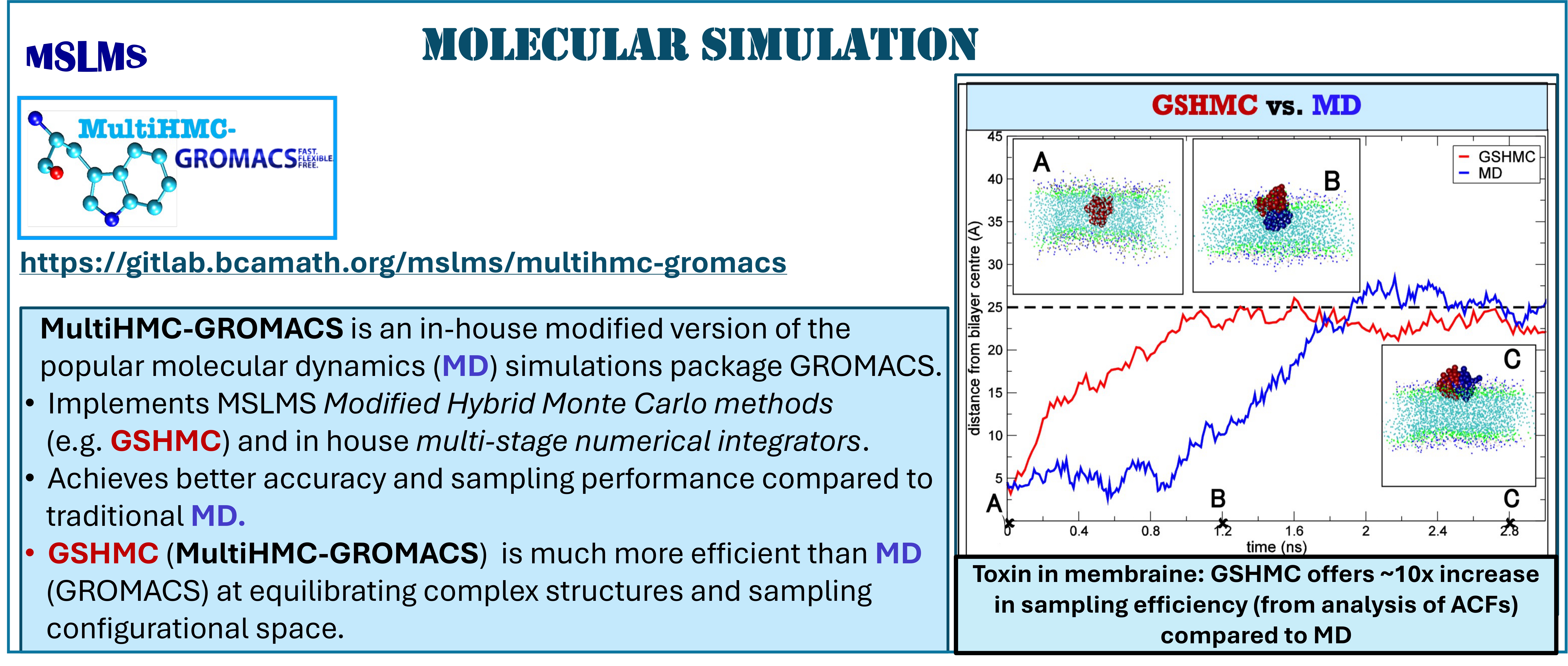
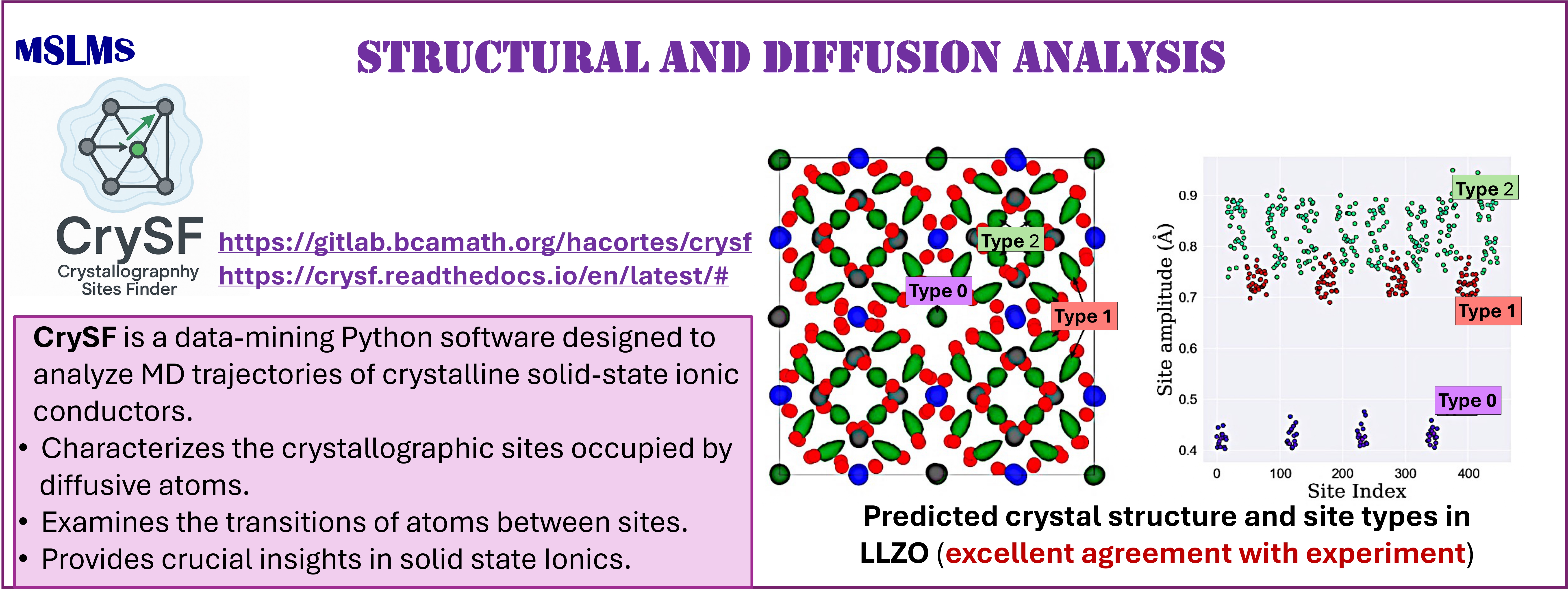

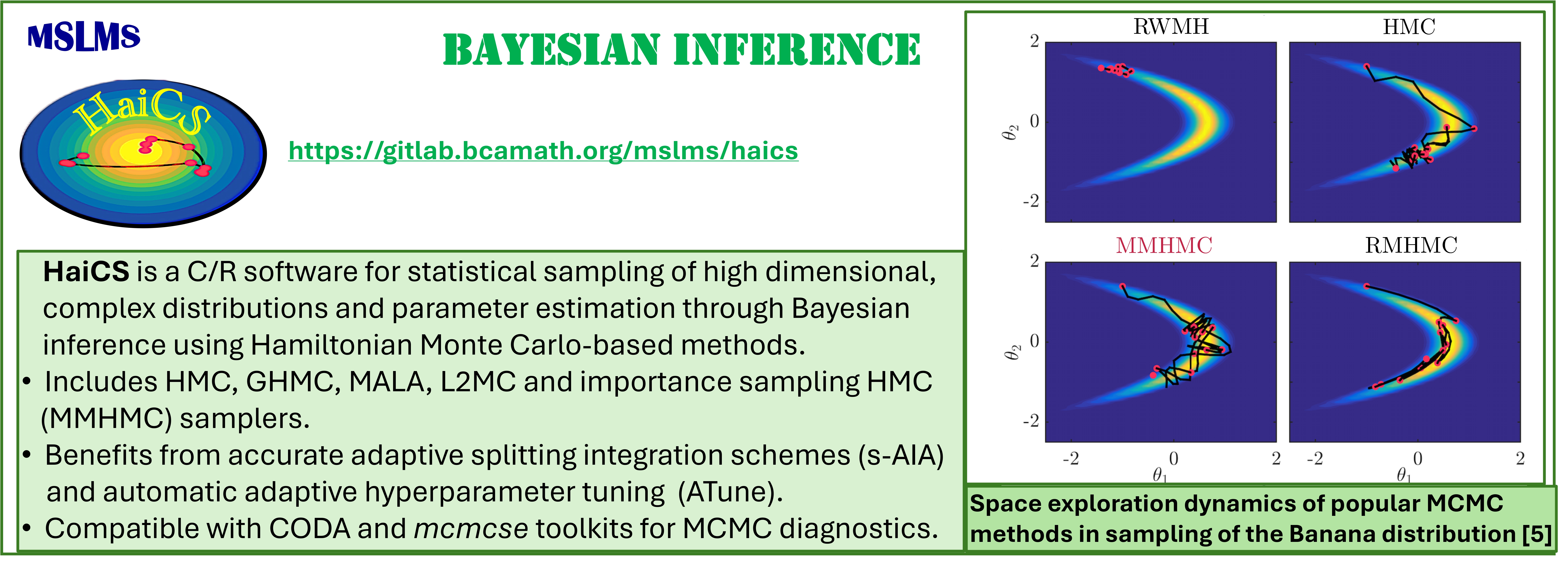
Modelling and Simulation
Modelling and simulation play a crucial role in theorizing and understanding complex systems. Our group employs the most efficient simulation techniques (in-house or external) to perform multiscale simulation of physical systems and Bayesian inference (Figure 9).
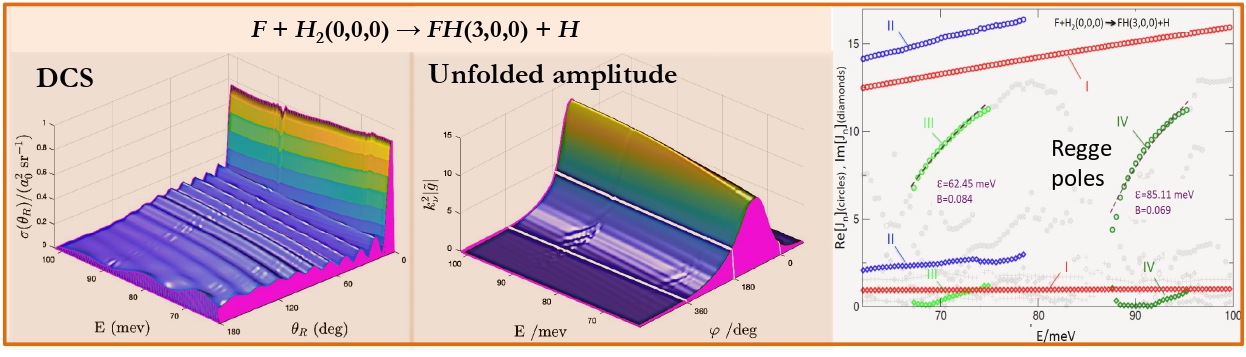
The computational models, proposed by the MSLMS are implemented in the MSLMS software packages and include the PBE model for study of formation and evolution of multi-phase polymer particles morphology [20] (Figure 10); the effective medium model for estimation of conductivities of cubic/tetragonal phase mixtures of solid electrolytes [26]; the CAM (Complex Angular Momenta Analysis) models for elastic, inelastic and reactive integral and differential cross sections in elementary chemical reactions [21-24] (Figure 11).
References
[1] Akhmatskaya E., Reich S. GSHMC: An Efficient Method for Molecular Simulation. Journal of Computational Physics 227 (2008) 4934 – 4954.
[2] Akhmatskaya E., Reich S. New Hybrid Monte Carlo Methods for Efficient Sampling: from Physics to Biology and Statistics. Progress in Nuclear Science and Technology 2 (2011) 447-462.
[3] Escribano B., Akhmatskaya E., Reich S., Azpiroz J.M. Multiple-time-stepping Generalized Hybrid Monte Carlo Methods. Journal of Computational Physics 280 1 (2015) 1 – 20.
[4] Fernández-Pendás M., Escribano B., Radivojević T., Akhmatskaya E. Constant Pressure Hybrid Monte Carlo Simulations in GROMACS. Journal of Molecular Modeling 20 (2014) 2487.
[5] Radivojevic T., Akhmatskaya E. Modified Hamiltonian Monte Carlo for Bayesian Inference. Statistics and Computing 30 (2020) 377-404.
[6] Sokolovski D., Rusconi S., Brouard S, Akhmatskaya E. Re-examination of Continuous Fuzzy Measurement on Two-level Systems. Phys. Rev. A 95 (2017) 042111.
[7] Sokolovski D., Rusconi S., Akhmatskaya E., Asua J.M. Non-Markovian Effects in the Growth of a Polymer Chain. Proceedings of the Royal Society A 471 (2015) 20140899.
[8] Rusconi S., Akhmatskaya E., Sokolovski D., Ballard N., de la Cal J.C. Relative Frequencies of Constrained Events in Stochastic Processes: an Analytical Approach. Phys. Rev. E 92 (4) (2015) 043306.
[9] Backman T.W.H., Schenk C., Radivojevic T., Ando D., Singh J., Czajka J.J., Costello Z., Keasling J.D., Tang Y., Akhmatskaya E., Garcia Martin H. BayFlux: A Bayesian Method to Quantify Metabolic Fluxes and their Uncertainty at the Genome Scale. PLOS Computational Biology 19(11) (2023) e1011111.
[10] Fernández-Pendás M., Akhmatskaya E., Sanz-Serna J.M. Adaptive Multi-stage Integrators for Optimal Energy Conservation in Molecular Simulations. Journal of Computational Physics 327 (2016) 434-449.
[11] Akhmatskaya E., Fernández-Pendás M., Radivojevic T., Sanz-Serna J.M. Adaptive Splitting Integrators for Enhancing Sampling Efficiency of Modified Hamiltonian Monte Carlo Methods in Molecular Simulation. Langmuir 33 (43) (2017) 11530-11542.
[12] Nagar L., Fernández-Pendás M., Sanz-Serna J.M., Akhmatskaya E. Adaptive Multi-stage Integration Schemes for Hamiltonian Monte Carlo. Journal of Computational Physics 502 (2024) 112800.
[13] Rusconi S., Dutykh D., Zarnescu A., Sokolovski D., Akhmatskaya E. An Optimal Scaling to Computationally Tractable Dimensionless Models: Study of Latex Particles Morphology Formation. Computer Physics Communications 247 (2020) 106944.
[14] García Daza F.A., Bonilla M.R., Llordés A., Carrasco J., Akhmatskaya E. Atomistic Insight into Ion Transport and Conductivity in Ga/Al-Substituted Li7La3Zr2O12 Solid Electrolytes. ACS Appl. Mater. Interfaces 11(1) (2019) 753-765.
[15] Bonilla M.R., García-Daza F., Cortés H.A., Carrasco J., Akhmatskaya E. On the Interfacial Lithium dynamics in Li7La3Zr2O12: Poly(ethylene oxide) (LiTFSI) Composite Polymer-ceramic Solid Electrolytes under Strong Polymer Phase Confinement. J. Colloid Interface Sci. 623 (2022) 870-882.
[16] Cortés H.A., Bonilla M.R., Marinero E., Carrasco J., Akhmatskaya E. Anion Trapping and Ionic Conductivity Enhancement in PEO-based Composite Polymer-Li7La3Zr2O12 Electrolytes: the Role of the Garnet Li Molar Content. Macromolecules 56 (2023) 4256-4266.
[17] Parga-Pazos M., Cusimano N., Rábano M., Akhmatskaya E., dM. Vivanco M. A Novel Mathematical Approach for the Analysis of Integrated Cell-patient Data Uncovers a 6-gene Signature Linked to Endocrine Therapy Resistance. Laboratory Investigation 104 (2024) 100286.
[18] Cortés H.A., Bonilla M.R., Akhmatskaya E. Unsupervised Density-based Method for Analysing Ion Mobility in Crystalline Solid-state Electrolytes. npj Comput Mater 11 (2025) 368.
[19] Ballard N., Rusconi S., Akhmatskaya E., Sokolovski D., de la Cal J., Asua J.M. The Impact of Competitive Processes on Controlled Radical Polymerization. Macromolecules 47 (19) (2014) 6580–6590.
[20] Rusconi S., Schenk C., Zarnescu A., Akhmatskaya E. Reducing Model Complexity by Means of the Optimal Scaling: Population Balance Model for Latex Particles Morphology Formation. Applied Mathematics and Computation (2022) 443 (2023) 127756.
[21] Sokolovski D., Akhmatskaya E., Sen S. Extracting Resonance Poles from Numerical Scattering Data: Type-II Padé Reconstruction. Computer Physics Communications 182 (2) (2011) 448-466.
[22] Akhmatskaya E., Sokolovski D., Echeverría-Arrondo C. Numerical Regge Pole Analysis of Resonance Structures in Elastic, Inelastic and Reactive State-to-state Integral Cross Sections. Computer Physics Communications 185 (7) (2014) 2127–2137.
[23] Akhmatskaya E., Sokolovski D. Numerical Regge Pole Analysis of Resonance Structures in State-to-state Reactive Differential Cross Sections. Computer Physics Communications 277 (2022) 108370.
[24] Sokolovski D., De Fazio D., Akhmatskaya E. A Transition State Resonance Radically Reshapes Angular Distributions of the F + H2 -> F H (vf = 3) + H Reaction in the 62.09-101.67 meV Energy Range. ACS Physical Chemistry Au 5(2) (2025) 219-226.
[25] Roell G., Schenk C., Anthony W., Carr R., Ponukumati A., Kim J., Akhmatskaya E., Foston M., Dantas G., Moon T.S., Tang Y., Garcia Martin H. A High-Quality Genome-Scale Model for Rhodococcus opacus Metabolism. ACS Synthetic Biology 12 (6) (2023) 1632-1644.
[26] Bonilla M.R., García Daza F., Carrasco J., Akhmatskaya E. Exploring Li-ion Conductivity in Cubic,Tetragonal and Mixed-phase Al-substituted LLZO Using Atomistic Simulations and Effective Medium Theory. Acta Materialia 175 (2019) 426-435.
Probabilistic Modelling of Classical and Quantum Systems
Adapting Hybrid Monte Carlo methods for solving complex problems in life and materials sciences
Enhancing Sampling in Computational StatisticsUsing Modified Hamiltonians
Pseudospectral methods and numerical continuation for the analysis of structured population models
Born model, Core-Shell model and Damped Shifted Force Coulomb sum codes compartible with LAMMPS and potfit GPL-licence packages for molecular simulations.
The Core-Shell model and the Damped Shifted Force (DSF) method for the Coulomb sum were added to the open source potfitforce-matching code, in order to allow the fitting of interatomic potentials from ab-initio data with this approaches.
The DSF method is already commited to the master branch of the code and will be released with the next stable version. The Core-Shell implementation is still in my local fork under testing and working on further features.
The Born model coupled to the Damped Shifted Force methods were added to the open source LAMMPS molecular dynamics code to perform dynamics consistent with the derived potentials, these changes are in my local fork but soon to be submitted to the master branch.
Authors: Ariel Lozano
License: GPL
Numerical Regge pole analysis of resonance structures in state-to-state reactive differential cross sections (DCS_Regge)
This is the third (and the last) code in a collection of three programs [Sokolovski et al. (2011), Akhmatskaya et al. (2014)] dedicated to the analysis of numerical data, obtained in an accurate simulation of an atom-diatom chemical reaction. Our purpose is to provide a detailed complex angular momentum (CAM) analysis of the resonance effects in reactive angular scattering. The code evaluates the contributions of a Regge trajectory (or trajectories) to a differential cross section in a specified range of energies. The contribution is computed with the help of the methods described in [Dobbyn et al. (1999), Sokolovski and Msezane (2004), Sokolovski et al. (2007)]. Regge pole positions and residues are obtained by analytically continuing S-matrix element, calculated numerically for the physical integer values of the total angular momentum, into the complex angular momentum plane using the PADE_II program [Sokolovski et al. (2011)]. The code represents a reactive scattering amplitude as a sum of the components corresponding to a rapid “direct” exchange of the atom, and the various scenarios in which the reactants form long-lived intermediate complexes, able to complete several rotations before breaking up into products.
Authors: Elena Akhmatskaya
License: the CPC non-profit use license agreement - Mendeley Data
Numerical Regge pole analysis of resonance structures in elastic, inelastic and reactive state-to-state integral cross sections (ICS_Regge)
ICS_Regge is a suite of FORTRAN codes for evaluation of the resonance contribution a Regge trajectory makes to the integral state-to-state cross section (ICS) within a specified range of energies. The contribution is evaluated with the help of the Mulholland formula (Macek et al., 2004) and its variants (Sokolovski et al., 2007; Sokolovski and Akhmatskaya, 2011). Regge pole positions and residues are obtained by analytically continuing S-matrix element, evaluated numerically for the physical values of the total angular momentum, into the complex angular momentum plane using the PADE_II program (Sokolovski et al., 2011). The code decomposes an elastic, inelastic, or reactive ICS into a structured, resonance, and a smooth, ‘direct’, components, and attributes observed resonance structure to resonance Regge trajectories.
Authors: Elena Akhmatskaya
License: the CPC non-profit use license agreement - Mendeley Data
Extracting S-matrix poles for resonances from numerical scattering data: type-II Padé reconstruction(PADE II)
The code is designed for evaluation of resonance pole positions and residues of a numerical scattering matrix element in the complex energy (CE) as well as in the complex angular momentum (CAM) planes. Analytical continuation of the S-matrix element is performed by constructing a type-II Pade approximant from given physical values. The algorithm involves iterative ‘preconditioning’ of the numerical data by extracting its rapidly oscillating potential phase component. The code has the capability of adding non-analytical noise to the numerical data in order to select ‘true’ physical poles, investigate their stability and evaluate the accuracy of the reconstruction. It has an option of employing multiple-precision (MPFUN) package developed by D.H. Bailey wherever double precision calculations fail due to a large number of input partial waves (energies) involved.
Authors: Elena Akhmatskaya
License: the CPC non-profit use license agreement - Mendeley Data
BayFlux
Bayesian Genome Scale 13C Metabolic Flux Analysis and Two Scale Metabolic Flux Analysis (2S-13C MFA). Co-development with Joint BioEnergy Institute (JBEI), Berkeley Lab, USA. The code also includes utilities for comparison of BayFlux with another established package called 13CFLUX2 which allow for automation of changing model’s input files, running the optimization, writing results to files for another software and reading from these files, and changing the inputs in an automatic way in BayFlux. This is implemented in several python and bash scripts: readfromxml.py with the changefml routine; script_automatechangefmlfile.py, script_automate13cflux2.sh and solsallinonecsvextended.py.
In addition, several functions for evaluation, plotting, and debugging purposes have been developed. Among these are enhancements to the validate function in cobrapy that is used in BayFlux and BayFlux's normpdf and logLikelihood function. Furthermore, an additional validatecheck of net samples was included that can optionally be turned on during sampling and can be extended to also checking directional fluxes. For plotting purposes several functions were added: overlap_density_plt, mdvboxplotwith13CFLUX2, paper_density_plt and enhanced: mdvboxplot, among others. We also added a routine to be able to provide simulated data as an input instead of real 13C data called simulated_data_as_input.
Jupyter notebooks illustrate the use of these developments for an E.coli model (including some additional tricks that can be used for debugging purposes.
Authors: Christina Schenk
License: Open source
PDE-HMC Interface
Bayesian inference combined with Advanced Hamiltonian samplers for parameterization of PDE models using a Finite-Volume solution scheme
Authors: Caetano Souto Maior Mendes
License: AGPL V3