MSLMS
Modelling and Simulation in Life and Materials Sciences
Our goal is to enable effective modelling and detailed simulation of complex systems & phenomena, which are not possible with existing simulation methods and often without high performance computers.
We are interested in devising reliable predictive tools for material science, biomedical applications, statistical inference and geophysics. The focus is on enhanced sampling stochastic/deterministic algorithms, numerical solution of (integro-) differential equations, machine-learning-driven algorithms and computational models.
MSLMS activities include the development of efficient numerical methods and algorithms, computational models, software and computational kits for simulations of complex systems, with an ultimate goal of applying them to real life problems. Multidisciplinary research and multitasking are two of the defining features of the MSLMS group.
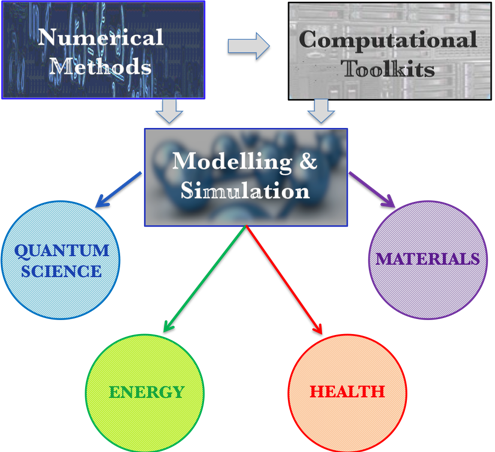
Figure 1. MSLMS actitivities
We develop numerical algorithms to mimic and accurately reproduce the properties of deterministic and stochastic computational models describing a wide range of phenomena.
Our methods (some of them are patented) aim to overcome the deficiencies of conventional techniques. We work on extension of the methods to a range of simulation scales and statistical ensembles. We also focus on further improvement of their efficiency through developing novel adaptive schemes, numerical integrators and parallel algorithms.
We disseminate the developed methodologies to a broad community of scientists and practitioners via open in-house software codes and computational toolkits co-developed in collaboration with our external partners. We also contribute to modernisation of well-established open source highly parallelized software packages.
Our group employs the most efficient simulation techniques (in-house or external) in order to perform multiscale simulation of physical systems and Bayesian inference.
Our researchers put into practice their mathematical expertise, helping answer the important practical questions arising in industry, environment, health and society (Figs. 2 - 3).
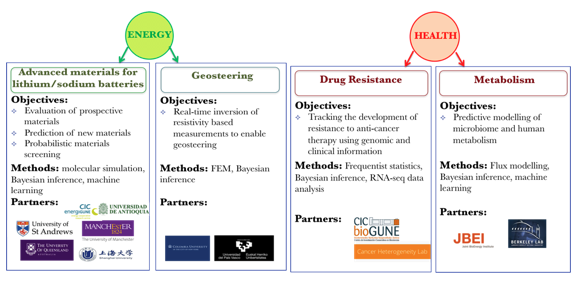
Figure 2. Applications in Energy and Health
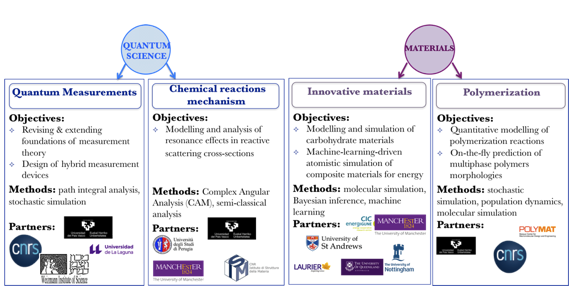
Figure 3. Applications in Quantum Science and Materials
Created in September 2010 and led by Ikerbasque Research Professor E. Akhmatskaya, the MSLMS group has been extended in 2021 with the ESM - BCAM Severo Ochoa Strategic Lab on Modelling with PDEs in Mathematical Biology headed by Prof. J.A. Carrillo (University of Oxford, UK). The research of the group and Lab is complementary (Figure 4).
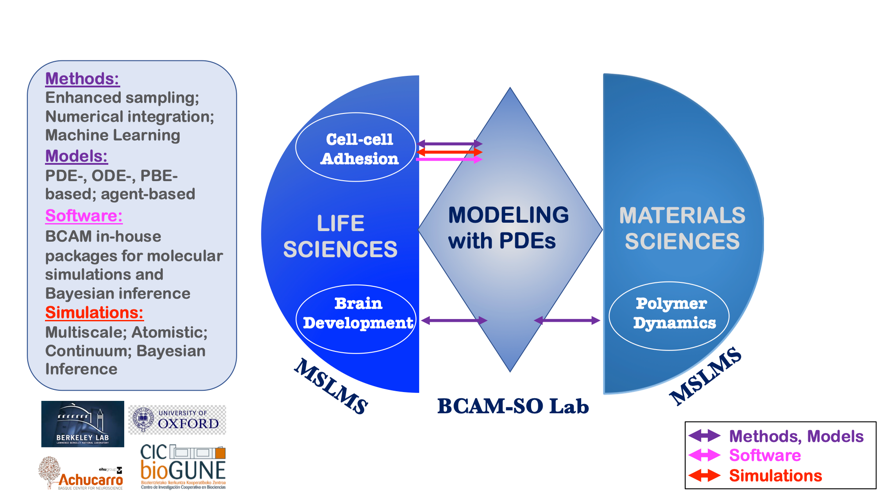
Figure 4. MSLMS-BCAM-So Lab synergy
Numerical Methods & Algorithms
Advanced numerical methods and algorithms can help applied scientists speed up simulations, improve their reliability and use most efficiently available High Performance Computing resources.
Enhanced sampling stochastic and deterministic algorithms
accurate sampling of high-dimensional spaces. If met, significant progress will be made in understanding many important phenomena in life and physical sciences.
Development of novel efficient Hamiltonian Monte Carlo (HMC) and Modified Hamiltonian Monte Carlo (MHMC) methods, which combine stochastic Markov Chain Monte Carlo (MCMC) with deterministic Hamiltonian Dynamics, is one of our long-standing research interests. Our first methods [1] of these two classes, patented in the US and GB, have clearly demonstrated their superiority in sampling performance over traditional sampling techniques, such as conventional MCMC, molecular dynamics (MD), Hybrid/Hamiltonian Monte Carlo (Figure 5). Today we work on adapting our methods to various simulation scales and statistical ensembles, in order to bridge the time, space and precision scale gaps between simulations and the phenomena of interest. The resulting methods - canonical, constant-pressure, grand-canonical, meso- and multiple-time-stepping variants [2] of HMC and MHMC as well as the Mix & Match HMC [3], developed specifically for Bayesian inference – aim at a wide range of applications.
In addition, we re-design original Monte Carlo algorithms to address particular challenges in applications of interest, e.g. polymerization reactions with delays, quantum measurements [4-5].
We also continue to improve performance of the developed samplers by introducing novel adaptive schemes, numerical integrators and parallel algorithms.
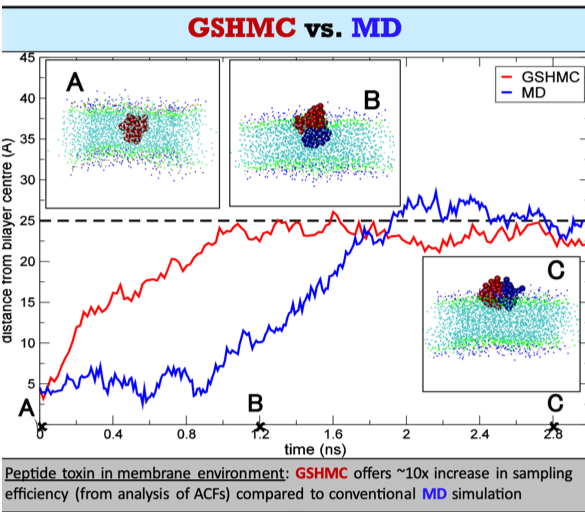

Figure 5. In-house MHMC (GSHMC) method vs. traditional sampling techniques for molecular simulation.
Numerical Integration
It often happens that differential equations, widely used in applied mathematics to describe various phenomena, do not have solutions expressible in closed form, and require numerical methods for finding approximate solutions.
Construction of robust and computationally efficient problem-specific integration schemes is, therefore, an important step in facilitating progress in fields as diverse as Classical and Quantum Mechanics, Materials Science, Biology or Engineering.
Common threads of topics we address are geometric integration and splitting algorithms.
Our objectives are to further theoretical knowledge on splitting integrators and other geometric methods, to construct new schemes and apply them to a number of fields. With that in mind, we develop new adaptive multi-stage splitting methods for molecular dynamics and (modified) Hamiltonian/Hybrid Monte Carlo sampling [6-7].
Combined with novel sampling techniques and computational models being introduced by the group, the integrators will make possible accurate modelling of very large complex systems of varied nature [8] (Figure 6). Currently, many such systems are beyond the capabilities of the existing modelling approaches.
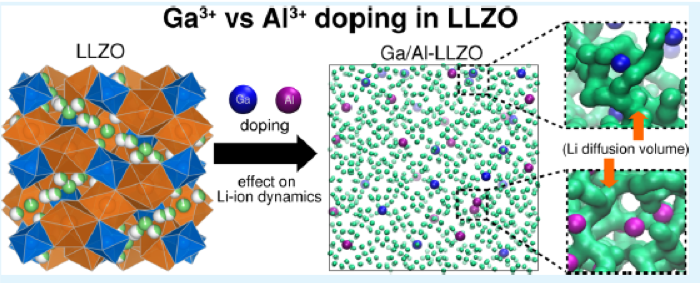
Figure 6. Ga3+ vs. Al3+ doping in LLZO: Using our enhanced MHMC sampler (GSHMC) combined with the adaptive modified splitting approach MAIA developed in MSLMS allowed us to explore, for the first time, the low-temperature region in atomistic simulations of metal-substituted garnet structured solid electrolytes. The study provides new insights into ion transport and conductivity in the promising solid electrolytes for next-generation solid-state Li batteries [8].
Machine-learning-driven approaches
We incorporate in our modelling methodologies various machine-learning-driven algorithms, to enable large-scale high-resolution simulation in energy and health applications. Bayesian and frequentist machine learning methods assist in performing global optimizations of molecular structures, and help to train atomistic force fields in simulation of energy materials. Machine learning algorithms also find their use in tuning performance and accuracy of the sampling techniques, applied for predictive modelling of microbiome and human metabolism, as well as in the analysis of clinical and RNA-Seq data for cancer research.
Computational Toolkits
Accurate prediction of complex physical and social processes is often impossible without full utilisation of the capabilities of modern HPC
The methodologies derived in MSLMS are implemented in the in-house or well-established open source software packages. MSLMS in-house computer codes include MultiHMC-GROMACS [6-7] (enhanced sampling Hybrid Monte Carlo methods in GROMACS package), LICA (postprocessing analysis of molecular dynamics trajectories), HaiCS [3] (statistical sampling and parameter estimation through Bayesian inference using Hamiltonian Monte Carlo methods), CRadPol (simulation of Controlled Radical Polymerization using experimental observations), Ddpm (simulation of dynamic development of particles morphology), ICS_Regge [9], DCS_Regge [10] (numerical Regge poles analysis of resonance structures in elastic, inelastic and reactive state-to-state integral and differential cross sections), PADE II [11] (type‐II Padé reconstruction of a scattering matrix element).
The computational models, proposed by the MSLMS, e.g., the PBE model for study of formation and evolution of multi-phase polymer particles morphology [12] (Figure 7); the effective medium model for estimation of conductivities of cubic/tetragonal phase mixtures of solid electrolytes [13]; the CAM (Complex Angular Momenta Analysis) models for elastic, inelastic and reactive integral and differential cross sections in elementary chemical reactions [9-11] (Figure 8), and the PDE magnetotelluric model for Bayesian inversion are implemented in the MSLMS software packages along with well-established models.
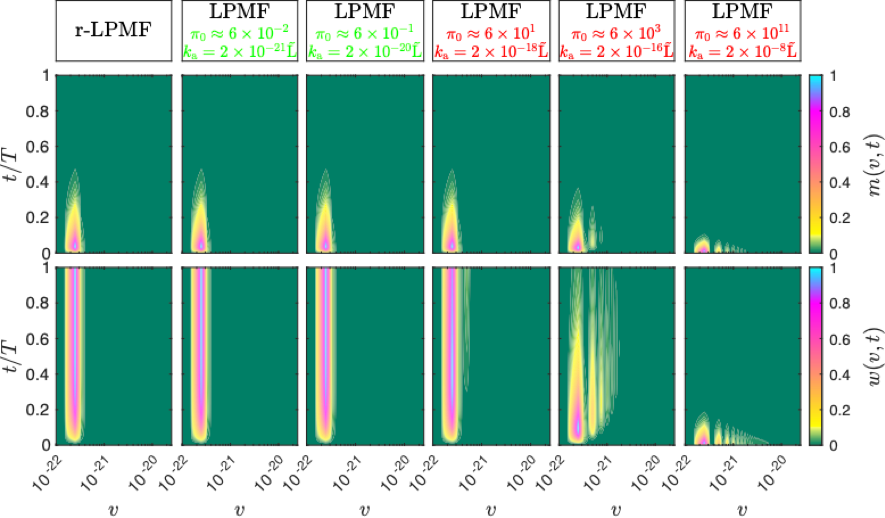
Figure 7. Our novel Population Balance Model for Latex Particles Morphology Formation of reduced complexity (r-LPMF) maintains the same level of accuracy for the identified range of parameters as a full LPMF model and requires up to 2 orders of magnitude less computational effort [12].
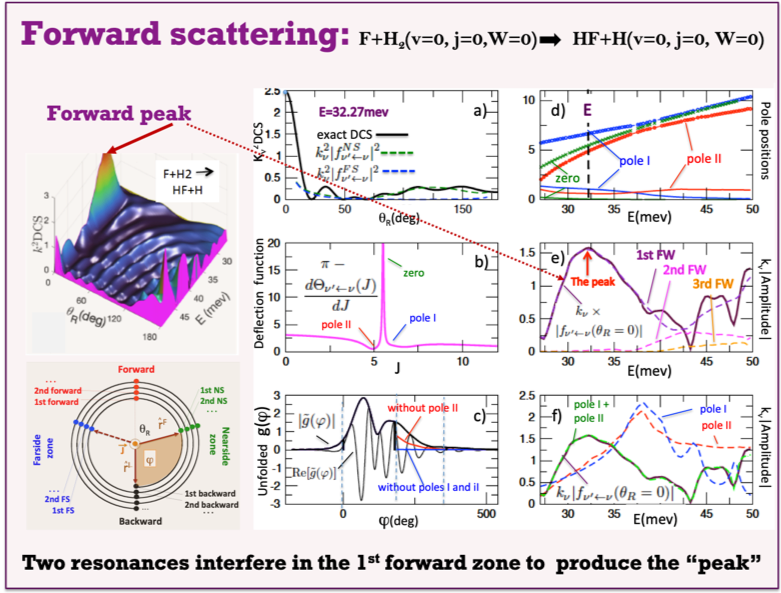
Figure 8. In-house package DCS_Regge allowed us to explain the origin of the forward peak, observed in the F+H2-> HF+H reaction [10].
Modelling and simulation
Modelling and simulation play a crucial role in theorizing and understanding complex systems. Our group employs the most efficient simulation techniques (in-house or external) in order to perform multiscale simulation of physical systems and Bayesian inference.
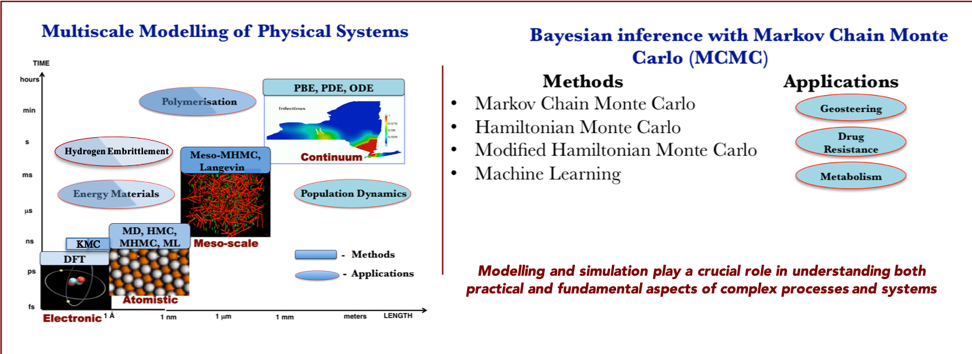
Figure 8. Modelling and simulation in MSLMS.
References
[1] Akhmatskaya E., Reich S. New Hybrid Monte Carlo Methods for Efficient Sampling: from Physics to Biology and Statistics. Progress in Nuclear Science and Technology 2 (2011) 447-462.
[2] Bonilla M.R., García Daza F., Fernández-Pendás M., Carrasco J., Akhmatskaya E. Multiscale Modelling and Simulation of Advanced Battery Materials. Progress in Industrial Mathematics: Success Stories, M. Cruz, C. Pares, P. Quintela (Eds), Springer, 69 – 113 (2021), ISBN 978-3-030-61843-8
[3] Radivojevic T., Akhmatskaya E. Modified Hamiltonian Monte Carlo for Bayesian Inference. Statistics and Computing 30 (2020) 377-404.
[4] Sokolovski D., Rusconi S., Brouard S, Akhmatskaya E. Reexamination of continuous fuzzy measurement on two-level systems. Phys. Rev. A 95 (2017) 042111.
[5] Sokolovski D., Rusconi S., Akhmatskaya E., Asua J.M. Non-Markovian effects in the growth of a polymer chain. Proceedings of the Royal Society A 471 (2015) 20140899.
[6] Fernández-Pendás M., Akhmatskaya E., Sanz-Serna J.M. Adaptive multi-stage integrators for optimal energy conservation in molecular simulations. Journal of Computational Physics 327 (2016) 434-449.
[7] Akhmatskaya E., Fernández-Pendás M., Radivojevic T., Sanz-Serna J.M. Adaptive splitting integrators for enhancing sampling efficiency of modified Hamiltonian Monte Carlo methods in molecular simulation. Langmuir 33 (43) (2017) 11530-11542.
[8] García Daza F.A., Bonilla M.R., Llordés A., Carrasco J., Akhmatskaya E. Atomistic Insight into Ion Transport and Conductivity in Ga/Al-Substituted Li7La3Zr2O12 Solid Electrolytes. ACS Appl. Mater. Interfaces 11(1) (2019) 753-765.
[9] Akhmatskaya E., Sokolovski D., Echeverría-Arrondo C. Numerical Regge pole analysis of resonance structures in elastic, inelastic and reactive state-to-state integral cross sections. Computer Physics Communications 185 (7) (2014) 2127–2137.
[10] Akhmatskaya E., Sokolovski D. Numerical Regge pole analysis of resonance structures in state-to-state reactive differential cross sections. Computer Physics Communications, 277 (2022) 108370.
[11] Sokolovski D., Akhmatskaya E., Sen S. Extracting Resonance Poles from Numerical Scattering Data: Type-II Padé Reconstruction. Computer Physics Communications 182 (2) (2011) 448-466.
[12] Rusconi S., Schenk C.,, Zarnescu A., Akhmatskaya E. Reducing model complexity by means of the Optimal Scaling: Population Balance Model for latex particles morphology formation. Applied Mathematics and Computation (2022).
[13] Bonilla M.R., García Daza F., Carrasco J., Akhmatskaya E. Exploring Li-ion conductivity in cubic, tetragonal and mixed-phase Al-substituted LLZO using atomistic simulations and effective medium theory. Acta Materialia 175 (2019) 426-435.
Probabilistic Modelling of Classical and Quantum Systems
Adapting Hybrid Monte Carlo methods for solving complex problems in life and materials sciences
Enhancing Sampling in Computational Statistics Using Modified Hamiltonians
Pseudospectral methods and numerical continuation for the analysis of structured population models
Born model, Core-Shell model and Damped Shifted Force Coulomb sum codes compartible with LAMMPS and potfit GPL-licence packages for molecular simulations.
The Core-Shell model and the Damped Shifted Force (DSF) method for the Coulomb sum were added to the open source potfitforce-matching code, in order to allow the fitting of interatomic potentials from ab-initio data with this approaches.
The DSF method is already commited to the master branch of the code and will be released with the next stable version. The Core-Shell implementation is still in my local fork under testing and working on further features.
The Born model coupled to the Damped Shifted Force methods were added to the open source LAMMPS molecular dynamics code to perform dynamics consistent with the derived potentials, these changes are in my local fork but soon to be submitted to the master branch.
Authors: Ariel Lozano
License: GPL
Numerical Regge pole analysis of resonance structures in state-to-state reactive differential cross sections (DCS_Regge)
This is the third (and the last) code in a collection of three programs [Sokolovski et al. (2011), Akhmatskaya et al. (2014)] dedicated to the analysis of numerical data, obtained in an accurate simulation of an atom-diatom chemical reaction. Our purpose is to provide a detailed complex angular momentum (CAM) analysis of the resonance effects in reactive angular scattering. The code evaluates the contributions of a Regge trajectory (or trajectories) to a differential cross section in a specified range of energies. The contribution is computed with the help of the methods described in [Dobbyn et al. (1999), Sokolovski and Msezane (2004), Sokolovski et al. (2007)]. Regge pole positions and residues are obtained by analytically continuing S-matrix element, calculated numerically for the physical integer values of the total angular momentum, into the complex angular momentum plane using the PADE_II program [Sokolovski et al. (2011)]. The code represents a reactive scattering amplitude as a sum of the components corresponding to a rapid “direct” exchange of the atom, and the various scenarios in which the reactants form long-lived intermediate complexes, able to complete several rotations before breaking up into products.
Authors: Elena Akhmatskaya
License: the CPC non-profit use license agreement - Mendeley Data
Numerical Regge pole analysis of resonance structures in elastic, inelastic and reactive state-to-state integral cross sections (ICS_Regge)
ICS_Regge is a suite of FORTRAN codes for evaluation of the resonance contribution a Regge trajectory makes to the integral state-to-state cross section (ICS) within a specified range of energies. The contribution is evaluated with the help of the Mulholland formula (Macek et al., 2004) and its variants (Sokolovski et al., 2007; Sokolovski and Akhmatskaya, 2011). Regge pole positions and residues are obtained by analytically continuing S-matrix element, evaluated numerically for the physical values of the total angular momentum, into the complex angular momentum plane using the PADE_II program (Sokolovski et al., 2011). The code decomposes an elastic, inelastic, or reactive ICS into a structured, resonance, and a smooth, ‘direct’, components, and attributes observed resonance structure to resonance Regge trajectories.
Authors: Elena Akhmatskaya
License: the CPC non-profit use license agreement - Mendeley Data
Extracting S-matrix poles for resonances from numerical scattering data: type-II Padé reconstruction(PADE II)
The code is designed for evaluation of resonance pole positions and residues of a numerical scattering matrix element in the complex energy (CE) as well as in the complex angular momentum (CAM) planes. Analytical continuation of the S-matrix element is performed by constructing a type-II Pade approximant from given physical values. The algorithm involves iterative ‘preconditioning’ of the numerical data by extracting its rapidly oscillating potential phase component. The code has the capability of adding non-analytical noise to the numerical data in order to select ‘true’ physical poles, investigate their stability and evaluate the accuracy of the reconstruction. It has an option of employing multiple-precision (MPFUN) package developed by D.H. Bailey wherever double precision calculations fail due to a large number of input partial waves (energies) involved.
Authors: Elena Akhmatskaya
License: the CPC non-profit use license agreement - Mendeley Data
BayFlux
Bayesian Genome Scale 13C Metabolic Flux Analysis and Two Scale Metabolic Flux Analysis (2S-13C MFA). Co-development with Joint BioEnergy Institute (JBEI), Berkeley Lab, USA. The code also includes utilities for comparison of BayFlux with another established package called 13CFLUX2 which allow for automation of changing model’s input files, running the optimization, writing results to files for another software and reading from these files, and changing the inputs in an automatic way in BayFlux. This is implemented in several python and bash scripts: readfromxml.py with the changefml routine; script_automatechangefmlfile.py, script_automate13cflux2.sh and solsallinonecsvextended.py.
In addition, several functions for evaluation, plotting, and debugging purposes have been developed. Among these are enhancements to the validate function in cobrapy that is used in BayFlux and BayFlux's normpdf and logLikelihood function. Furthermore, an additional validatecheck of net samples was included that can optionally be turned on during sampling and can be extended to also checking directional fluxes. For plotting purposes several functions were added: overlap_density_plt, mdvboxplotwith13CFLUX2, paper_density_plt and enhanced: mdvboxplot, among others. We also added a routine to be able to provide simulated data as an input instead of real 13C data called simulated_data_as_input.
Jupyter notebooks illustrate the use of these developments for an E.coli model (including some additional tricks that can be used for debugging purposes.
Authors: Christina Schenk
License: Open source
PDE-HMC Interface
Bayesian inference combined with Advanced Hamiltonian samplers for parameterization of PDE models using a Finite-Volume solution scheme
Authors: Caetano Souto Maior Mendes
License: AGPL V3
