MTB

Our research group is currently working on:

COVID19:

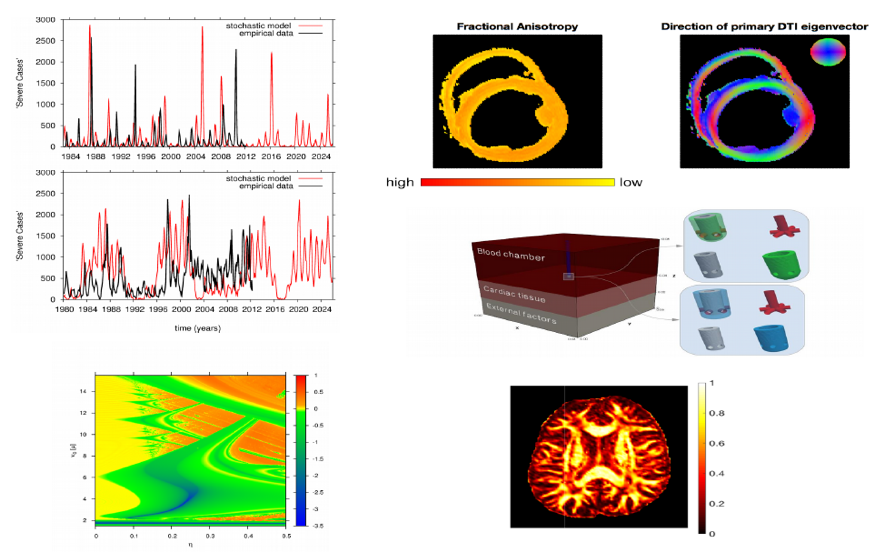
We model the dynamics of the corona virus disease 2019 (COVID-19) to describe the impact of the COVID19 pandemic in the Basque Country and other European regions. To describe accurately the process of disease spreading we use the SHARUCD model (susceptible (S), hospitalized (H) including all severe cases, asymptomatic (A) that includes also sub-clinical or mild infections, recovered (R), patients admitted to the intensive care units (U) from the recorded cumulative positive cases (C) which includes all new positive cases for each class, and death (D)).

The model was able to describe well the available empirical data on disease incidence and was tested on short term predictions for the exponential phase of the epidemics that was happening at least until March 25th, 2020. With a good agreement with later updated data, we observed that the epidemic in the Basque Country has now entered the linear phase, where the new number of cases are increasing lees and stabilizing. We now monitor the effect of the control measures on the infectivity of the population in order to give a longer term prediction of the epidemic and discuss the future decisions on relaxing the social distancing measures which are still in place.

Public Health Epidemiology:

Mathematical modeling is an important tool for the understanding of infectious disease epidemiology and dynamics, leading to great advances in providing tools for identifying possible approaches to control disease transmission and for assessing the potential impact of different public health intervention measures. Focused on basic and applied aspects of host, pathogen, and environmental factors that influence disease emergence, transmission and spread, epidemiological models are formulated to describe the transmission of the disease and to predict future outbreaks, addressing specific public health questions on disease epidemiology, prevention and control.

M. Aguiar (Research Line Leader, Ikerbasque Researcher) has large experience in modeling infectious diseases dynamics with focus in dengue fever epidemiology. Multi-strain dengue dynamics have been modeled with extended Susceptible-Infected-Recovered (SIR)-type models including immunological aspects of the disease such as the Antibody Dependent-Enhancement (ADE) phenomenology; Maira has investigated a minimalist twoinfection dengue model, with at least two different dengue serotypes to describe differences between primary and secondary infections [1,2]. Deterministic chaos was found in much wider parameter regions (not predicted by previous models), no longer needing to restrict the infectivity on a secondary infection to be much larger than the infectivity on primary infection. The minimalistic model successfully described large fluctuations observed in empirical outbreak data, estimating lower infection rate for secondary dengue infections than for primary infections[1-3], anticipating results published recently in Duong et al. PNAS 2015. Aguiar has also shown that the combination of immunological aspects of the disease such as temporary cross-immunity (TCI) and ADE are the most important features to drive the complex dynamics in the system, more than the detailed number of serotypes to be added in the model [3]. However, this work is focusing on the multi-strain aspect of the disease and its effects on the host population only, taking effects of the vector dynamics into account only by the model parameters. Regarding the newly licensed dengue vaccine, opposing the predictions made by other groups, Aguiar et al. have discussed the risks behind this vaccine recommendation [4], after analyzing an age-structured model [5]. Using the publicly available vaccine trial data, vaccine efficacy was estimated via the Bayesian approach, predicting a significant reduction of hospitalizations only when the vaccine is given to seropositive individuals [6-9]. This work is still ongoing and includes research on:

i) infectious disease transmission dynamics and prediction; ii) infectious disease control (including vector control and vaccination, with eventual industry collaboration), iii) epidemiological dynamics of multi-strain infectious diseases, iv) interplay between pathogen serotypes and cross-immunity, v) epidemiological dynamics of vaccine preventable diseases, vi) epidemiological dynamics of vector-pathogen-host interaction [10], vii) within-host dynamics focusing on immune responses, viii) complex dynamics, empirical data analysis and public health intervention measures.

Models are parameterized on disease incidence data considering the prevalence of infection in different endemic countries. A combination of techniques, including non-linear time series analysis, classical bifurcation diagrams and Lyapunov exponent spectra are used.

 

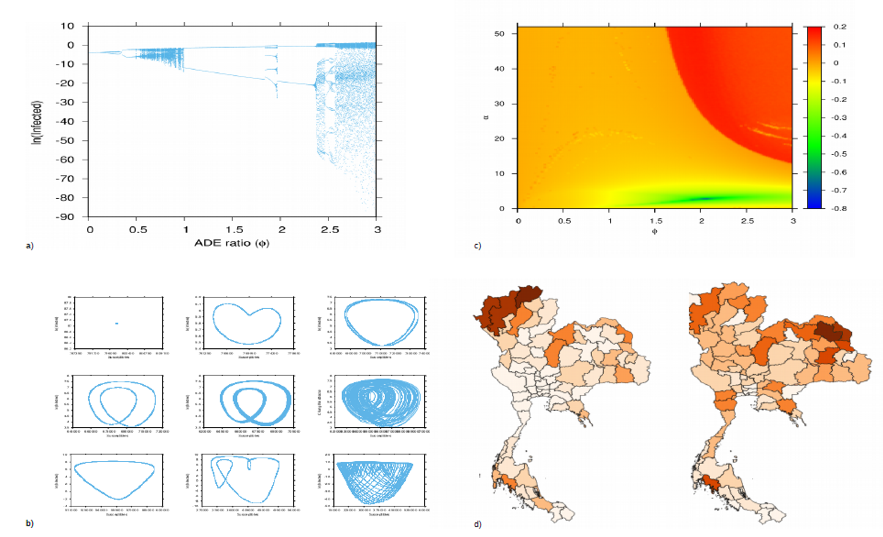
Compilation of different analyses of multi-strain complex systems. In a) Bifurcation diagram showing two chaotic windows in wide parameter regions for the minimalistic multi-strain dengue model. In b) state space analyses of attractors found during the bifurcation analysis performed in a). In c) 2D Lyapunov spectra used to evaluate the prediction horizon of a simple 2-infection dengue model. In d) Spatial temporal pattern of dengue disease spreading in Thailand.

Population dynamics and methodological topics in natural sciences and mathematics:

i) Time-scale separation and center manifold analysis describing vector-borne disease dynamics

In vector-borne diseases, the human hosts epidemiology often acts on a much slower time scale than the one of the mosquitoes transmitting as a vector from human to human, due to their vastly different life cycles. We investigate in how far the fast time scale of the mosquito epidemiology can be slaved by the slower human epidemiology, so that for the understanding of human disease data mainly the dynamics of the human time scale of immunological status is essential and only slightly perturbed by the mosquito dynamics [11].

ii) Stochastic processes and spatially extended systems

We describe spreading of diseases in geographical space via super-diffusion. Nowadays people travel a lot over wide distances and therefore the spread of the infection happens not only locally, i.e., from one person to the neighbor, but also for large distances. Super-diffusion has been suggested to model this type of epidemiological spreading in space. We consider the analytically tractable case of a diffusion like process on the lattice which is used as a surrogate process of human contacts in epidemiology. A stochastic process for a population is then used where the notion of distance is given by power law decaying connectivities, in good agreement with the analytics.

For dengue fever, good empirical data are available for different endemic countries. We develop spatial extended systems to investigate disease transmission and the impact of disease control.

iii) Bio-statistics, model comparison and parameter estimation of chaotic systems

The parameter estimation framework for population biological dynamical systems are applied to calibrate the models developed. Initial studies have been performed, partly on analytically solvable simple models, now ready for application also to complex system as investigated here. For parameter estimation in complex dynamical multi-strain models, a novel and ambitious application of recently developed techniques for parameter estimation for chaotic systems, a method called maximum likelihood iterated filtering (MIF) is being implemented and refined by including dynamic noise in likelihood functions for multi-strain dynamics. Indeed, understanding how stochasticity interacts with the deterministic components of epidemiological models would have important benefits on the practical predictability of the dynamical systems. To be predictive and not include unnecessary components in the mathematical models used, parsimony is important. Statistical methods are complemented with dynamical insight into the processes, in order to obtain biologically relevant parameter regions. New tools of non-linear data analysis like Takens embedding are available, and allow to obtain topological information (fixed points, periodic orbits and the nature of chaotic attractors) about the whole multi-strain epidemiological system from time series of overall infected only.

Besides using maximum likelihood methods and Bayesian approaches for the estimation of parameters, especially the Bayesian framework which gives normalized probabilities not only for parameters conditioned on given data, we also work with probabilities for different models conditioned on the same data.

 

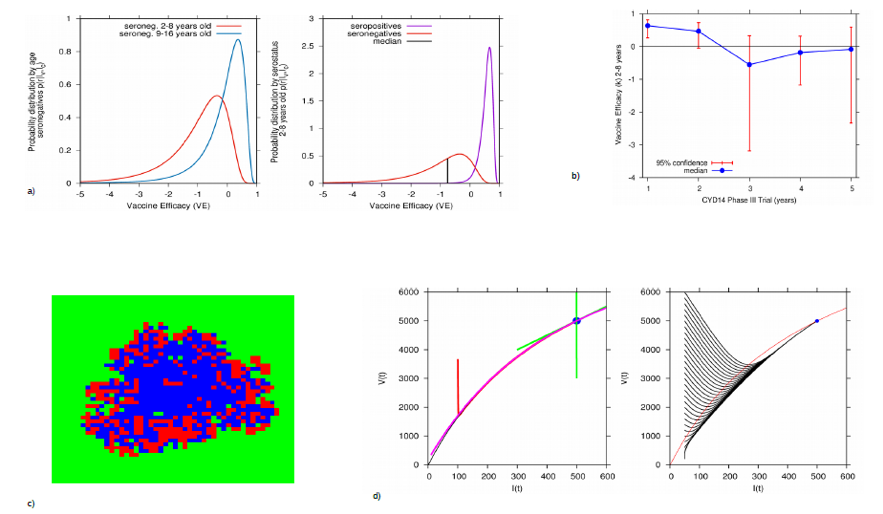
Compilation of different analyses. Using the Bayesian approach, in a) vaccine efficacy distribution by serostatus and age. In b) vaccine efficacy estimation changing over time, likely to be related to waining immunity. In c) a spatially extended stochastic simulation for reinfection models and in d) time scale separation of mosquito infection and human infection.

Physiological and Medical Systems:

(Keywords: non-local electrophysiology, brain tumor modeling, radio frequency ablation)

N. Cusimano (BCAM Post-doctoral fellow; non-local electrophysiology). Nicole has a solid background in electrophysiology and one of the main foci of her research has been the use of fractional order differential operators to describe electrical signal propagation in complex biological media characterized by high levels of heterogeneity (e.g., cardiac tissue) [12]. More theoretical aspects of her research involve the study of numerical methods for the discretization of fractional powers of elliptic operators and the solution of the corresponding fractional partial differential equations [13]. Nevertheless, she is particularly interested in merging theoretical results and experimental data [14]. To this end, she has recently started investigating different uncertainty quantification strategies, exploring both simulation-based methodologies for forward uncertainty propagation and Bayesian approaches to inverse uncertainty quantification.

 

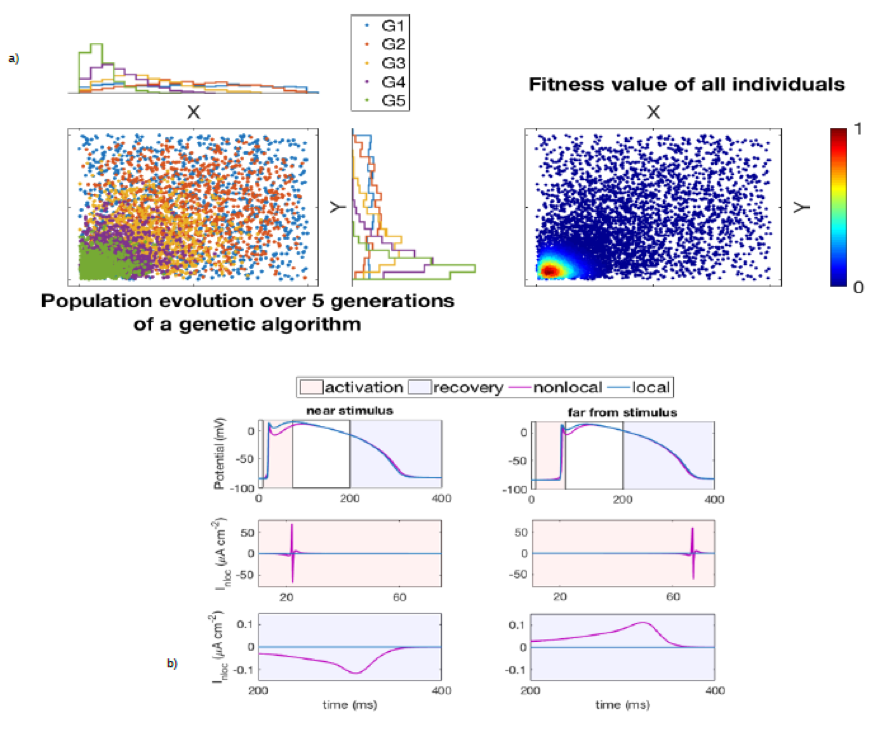
In a) Starting from an initial pool of candidate parameter sets, a genetic algorithm uses its characteristic operations (selection, crossover, and mutation) to evolve the population over successive generations and explore the parameter space. The figure shows the evolution of G1 over five successive generations (left) and the fitness value assigned to all individuals in the considered five populations (right).

In b) The non-local diffusion term in the spacefractional model of cardiac electrophysiology can be seen as the sum of standard diffusion (corresponding to an ideally homogeneous tissue) and a hypothetical non-local current quantifying the effect of tissue heterogeneities on excitation dynamics. This figure shows the differences in the local and non-local case, at two different spatial locations, in the action potential of the Beeler-Reuter model (top row) and in the non-local current during activation (mid row) and recovery (bottom row).

M. Conte (La Caixa PhD student - INPhINIT 2017; brain tumor modeling). Martina is working on multiscale models for brain tumor, studying the phenomenon of tumor cell invasion into the healthy tissue, a complex process involving several scales, from the description of microscopic intracellular dynamics to the behaviours of individual cells, and up to the macroscopic tumor density evolution. In particular, Martinas PhD Project focuses on the development of different mathematical models for the description of tumor growth and spread inside the brain. Multiscale approaches and kinetic methods are used to gain insight into the process of tumor cell migration, particularly in relation to the anisotropic character of the brain tissue and to the influence of several tumor microenvironment components. A relevant part of her research concerns numerical simulations of the models and data analysis. Martina is particularly interested in including in the models real data on brain geometry and cell diffusivity (MRI and DTI data), as well as experimental data on the interactions between the tumor and its microenvironment. This represents a fundamental step towards the model validation and is a key aspect in the quantitative and predictive analysis of the model outcomes.

 

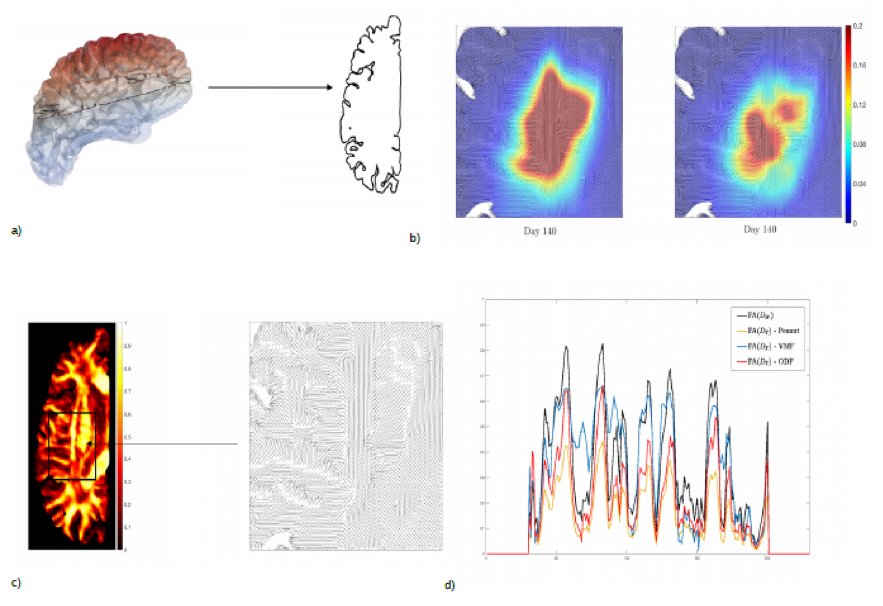
In a) Reconstruction of the left hemisphere of the brain visualized with Paraview (left) and the contour of one slice of the brain (right), representing the computational domain for the numerical simulations.

In b) Simulation of the tumor evolution after 140 days together with the fiber direction: comparison between a purely diffusive model, with anisotropic diffusion tensor (left plot) and an advection-diffusion model (right plot). The latter is obtained using a multiscale approach and including the description of microscopic integrin dynamics.

In c) Fractional anisotropy of the Water Diffusion Tensor (D_W(x)) (left) and visualization of the fiber tracts in the selected subdomain (right), and in d) Comparison between the Fraction Anisotropy (FA) of the Water Diffusion Tensor (D_W(x)) and of the Tumor Diffusion Tensor (D_T(x)) along a coronal plane of a 2D brain slice. D_T(x) is obtained using three different fiber distribution functions: Peanut distribution, Von Mises-Fisher distribution (VMF) and Orientation Distribution Function (ODF).

M. Echeverria Ferrero (PhD Student "Predoc. Severo Ochoa" 2018; radio frequency ablation). Marinas PhD thesis will consist of developing a patientspecific mathematical model for the treatment of cardiac arrhythmias. As an extension of [Petras, A. (2019). A computational model of open irrigated radio frequency catheter ablation accounting for mechanical properties of the cardiac tissue. International journal for numerical methods in biomedical engineering], the model will include both real geometries from medical imaging and realistic features of a medical procedure called radio frequency catheter ablation (RFCA), e.g., efficiently simulate the effect of catheter movement during the ablation procedure at different ablation sites, through simulations of RFCA. The mathematical model addresses the physical phenomena regarding the interaction between the RF energy and the cardiac tissue by means of Partial Differential Equations, which are solved numerically in an open-source Finite Element platform.

 

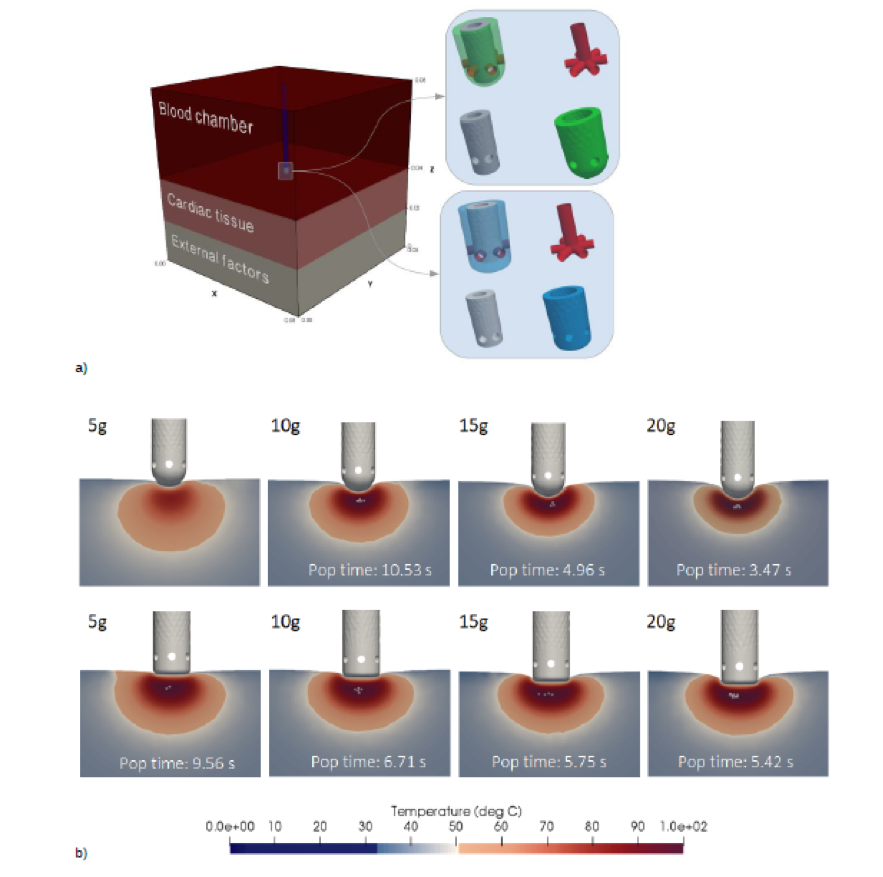
In a) Full 3D computational geometry. Right: detail of the computational catheter tips: the assembled catheter tip (top left), the saline pipes (top right), the thermistor (bottom left) and the electrode (bottom right). Green color for hemispherical catheter tip, blue for cylindrical.

In b) Lateral slices of the created lesion for spherical (top row) and cylindrical (bottom row) simulations, for catheter insertion forces of 5g, 10g, 15g and 20g. The pops in the tissue are highlighted as gray spheres (bubbles) and the popping time (in seconds) is indicated.

Selected Publications:

[1] Aguiar, M., Ballesteros, S., Kooi, B.W. & Stollenwerk, N. (2011). The role of seasonality and import in a minimalistic multi-strain dengue model capturing differences between primary and secondary infections: complex dynamics and its implications for data analysis. Journal of Theoretical Biology, 289, 181-196.

[2] Aguiar, M., Stollenwerk, N. & Kooi, W.B. (2012). Scaling of stochasticity in dengue hemorrhagic fever epidemics. Mathematical Modelling of Natural Phenomena, 7, 1-11.

[3] Aguiar, M., Kooi, W.B., Rocha, F., Ghaffari, P. & Stollenwerk, N. (2013). How much complexity is needed to describe the fluctuations observed in dengue hemorrhagic fever incidence data? Ecological Complexity, 16, 31-40.

[4] Aguiar, M., Stollenwerk, N. & Halstead S.B. (2016). The risks behind Dengvaxia recommendation. The Lancet Infectious Diseases, 16, 882-883.

[5] Aguiar, M., Stollenwerk N. & Halstead, S.B. (2016). Modeling the impact of the newly licensed dengue vaccine in endemic countries, PLoS Neglected Tropical Diseases, 10(12), e0005179.

[6] Aguiar, M., Halstead, S.B. & Stollenwerk, N. (2017). Consider stopping dengvaxia administration without immunological screening. Expert Review of Vaccines, 16 (4), 301-302.

[7] Aguiar, M. (2018). Dengue vaccination: a more ethical approach is needed. The Lancet, 391(10132), 1769-1770.

[8] Aguiar, M. & Stollenwerk, N. (2018). Dengvaxia: age as surrogate for serostatus. The Lancet Infectious Diseases, 18(3), 245.

[9] Aguiar, M. & Stollenwerk, N. (2018). Dengvaxia efficacy dependency on serostatus: a closer look at more recent data. Clinical Infectious Diseases, 66(4), 641-642.

[10] Rashkov, P., Venturino, E., Aguiar, M., Stollenwerk, N. & Kooi, B.W. (2019). On the role of vector modeling in a minimalistic epidemic model. Mathematical Biosciences and Engineering,16(5):4314-4338

[11] Rocha, F., Aguiar, M., Souza, M. & Stollenwerk, N. (2013). Time scale separation and center manifold analysis describing vector borne diseases dynamics. International Journal of Computer Mathematics, 90, 2105-2125.

[12] Cusimano, N., Gizzi, A., Fenton, F.H., Filippi, S.,& Gerardo-Giorda, L. (2020). Key aspects for effective mathematical modelling of fractional diffusion in cardiac electrophysiology: A quantitative study. Communications in Nonlinear Science and Numerical Simulation, 84, 105152.

[13] Cusimano, N., del Teso, F. & Gerardo-Giorda, L. (forthcoming). Numerical approximations for fractional elliptic equations via the method of semigroups. ESAIM: Mathematical Modeling and Numerical Analysis.

[14] Drovandi, C.C., Cusimano, N., Psaltis, S., Lawson, B.A.J., Pettitt, A.N., Burrage, P. & Burrage, K. (2016). Sampling methods for exploring between-subject variability in cardiac electrophysiology experiments. Journal of the Royal Society Interface, 13, 20160214.

[15] Conte, M., Gerardo-Giorda, L. & Groppi, M. (2020). Glioma invasion and its interplay with nervous tissue and therapy: A multiscale model. Journal of theoretical biology, 486, 110088.