Mathematics of the quantum many–body problem and condensed matter physics

The understanding of quantum phenomena in condensed matter physics, like superfluidity or Bose-Einstein condensation (see Figure 1.), represents one of the most challenging problems in modern physics, requiring new experimental and mathematical studies. Rigorous quantum many-body theory is however, a notoriously difficult subject. The hurdles that have to be overcome in order to arrive at important new mathematical results involve many different fields of mathematics such as probability theory, operator algebras, differential equations or functional analysis. I will therefore present a synthetic view of the mathematics of the quantum many-body problem in relation to my findings from the past 10 years. In particular, I will give an overview of the mathematics of ultra-cold quantum systems related to Brownian motions, large deviations, variational problems and C*-algebras. I will also provide a record of new mathematical tools I am developing with my co-authors to analyze complex phenomena (for instance, the flow equations for unbounded operators).

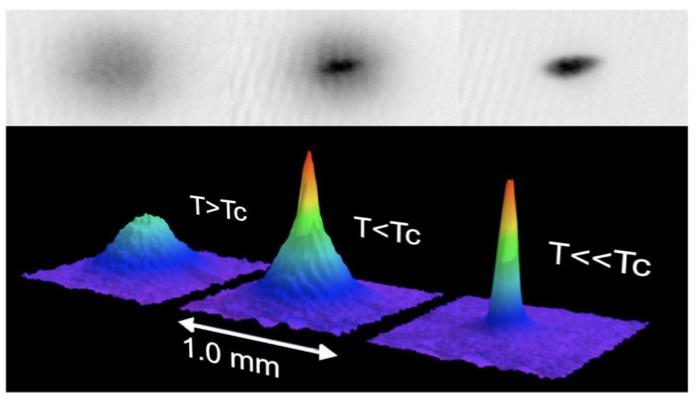
Figure1. Bose-Einstein condensation for temperatures <<10^-5 K performed for ²³Na in the MIT by the group of Wolfgang Ketterle (Nobel Prize Physics). The colours indicate the number of atoms at each velocity (red is the lowest velocity).