
T
+34 946 567 842
F
+34 946 567 842
E
lvega@bcamath.org
Information of interest
- Orcid: 0000-0001-5086-6345
My research is mainly focused in the interplay of Fourier Analysis and Partial Differential Equations of Mathematical Physics. More recently on fluid mechanics and turbulence. Concretely in the so called Localized Induction Approximation, also known as the binormal curvature flow (BF), for the evolution of vortex filaments and the relevance of the presence of corners in the filament. The results concerning regular polygons seem to me quite striking. Motivated by a numerical experiment done by D. Smets, and together with F. De La Hoz, we established in 2014 a numerical connection between the trajectory followed by a corner of, say an equilateral triangle, and a classical analytical problem that goes back at least to Riemann: the existence of continuous functions which are no where differentiable. Very recently (arXiv:2007.07184), and in collaboration with V. Banica, we have proved analytically that this connection is indeed true.
Right now I am also working together with N. Arrizabalaga and A. Mas, on relativistic and non-relativistic equations with singular electromagnetic potentials. The singularities of the potentials are critical from the point of view of the scaling symmetry. In the relativistic setting we consider perturbations of Dirac equation given by singular measures supported on smooth hyper-surfaces. This mathematical problem is closely related to a relevant question in physics, that of the optimal confinement of relativistic quantum particles.
Finally I continuous working on the deep connection between uncertainty principles, that are easily described using the Fourier transform, and lower bounds for solutions of linear and non-linear dispersive equations. This is a topic that I started with L. Escauriaza, Carlos E. Kenig and G. Ponce more than 10 years ago and from which very fruitful branches have emerged. For example, one of the first consequences we obtained using these lower bounds, was that a compact perturbation of a solitary wave or soliton of the Korteweg-De Vries (KdV) equation instantaneously destroys its exponential decay. KdV is a simplified local model about the dynamics of the frontier of a fluid. In particular, it describes with very high accuracy the propagation of a wave along a narrow and sallow channel. However, when the depth is big so that it can be considered close to be infinite the local approximation is too rough and non-local models as the Benjamin-Ono equation has to be considered. It turns out that the answer to the corresponding question requires completely different techniques that are closer to those developed with A. Fernández-Bertolin for the discrete laplacian and with L. Roncal and D. Stan for the fractional laplacian.
-
On low regularity well-posedness of the binormal flow
(2025)Abstract. We focus on a class of solutions of the binormal flow, model of the evolution of vortex filaments, that generate several corner singularities in finite time. This phenom- enon has been studied in [4, 1] in the ...
-
Blow-up for the 1D cubic NLS
(2023)We consider the 1D cubic NLS on ℝ and prove a blow-up result for functions that are of borderline regularity, i.e. Hs for any s<−12 for the Sobolev scale and L∞ for the Fourier-Lebesgue scale. This is done by identifying ...
-
The Frisch–Parisi formalism for fluctuations of the Schrödinger equation
(2022)We consider the solution of the Schrödinger equation $u$ in $\mathbb{R}$ when the initial datum tends to the Dirac comb. Let $h_{\text{p}, \delta}(t)$ be the fluctuations in time of $\int\lvert x \rvert^{2\delta}\lvert ...
-
Static and Dynamical, Fractional Uncertainty Principles
(2021-03)We study the process of dispersion of low-regularity solutions to the Schrödinger equation using fractional weights (observables). We give another proof of the uncertainty principle for fractional weights and use it to get ...
-
Eigenvalue Curves for Generalized MIT Bag Models
(2021)We study spectral properties of Dirac operators on bounded domains Ω ⊂ R 3 with boundary conditions of electrostatic and Lorentz scalar type and which depend on a parameter τ ∈ R; the case τ = 0 corresponds to the MIT ...
-
Unbounded growth of the energy density associated to the Schrödinger map and the binormal flow
(2021)We consider the binormal flow equation, which is a model for the dynamics of vortex filaments in Euler equations. Geometrically it is a flow of curves in three dimensions, explicitly connected to the 1-D Schr¨odinger map ...
-
On the one dimensional cubic NLS in a critical space
(2021)In this note we study the initial value problem in a critical space for the one dimensional Schr¨odinger equation with a cubic non-linearity and under some smallness conditions. In particular the initial data is given by ...
-
On the improvement of the Hardy inequality due to singular magnetic fields
(2020-09-01)We establish magnetic improvements upon the classical Hardy inequality for two specific choices of singular magnetic fields. First, we consider the Aharonov-Bohm field in all dimensions and establish a sharp Hardy-type ...
-
On the unique continuation of solutions to non-local non-linear dispersive equations
(2020-08-02)We prove unique continuation properties of solutions to a large class of nonlinear, non-local dispersive equations. The goal is to show that if (Formula presented.) are two suitable solutions of the equation defined in ...
-
Riemann's non-differentiable function and the binormal curvature flow
(2020-07-14)We make a connection between a famous analytical object introduced in the 1860s by Riemann, as well as some variants of it, and a nonlinear geometric PDE, the binormal curvature flow. As a consequence this analytical object ...
-
Vortex Filament Equation for a regular polygon in the hyperbolic plane
(2020-07-09)The aim of this article is twofold. First, we show the evolution of the vortex filament equation (VFE) for a regular planar polygon in the hyperbolic space. Unlike in the Euclidean space, the planar polygon is open and ...
-
On the energy of critical solutions of the binormal flow
(2020-07-02)The binormal flow is a model for the dynamics of a vortex filament in a 3-D inviscid incompressible fluid. The flow is also related with the classical continuous Heisenberg model in ferromagnetism, and the 1-D cubic ...
-
Evolution of Polygonal Lines by the Binormal Flow
(2020-06-01)The aim of this paper is threefold. First we display solutions of the cubic nonlinear Schrödinger equation on R in link with initial data a sum of Dirac masses. Secondly we show a Talbot effect for the same equation. Finally ...
-
Asymptotics in Fourier space of self-similar solutions to the modified Korteweg-de Vries equation
(2020-05-01)We give the asymptotics of the Fourier transform of self-similar solutions for the modified Korteweg-de Vries equation. In the defocussing case, the self-similar profiles are solutions to the Painlevé II equation; although ...
-
Uniqueness properties of solutions to the Benjamin-Ono equation and related models
(2020-03-15)We prove that if u1,u2 are real solutions of the Benjamin-Ono equation defined in (x,t)∈R×[0,T] which agree in an open set Ω⊂R×[0,T], then u1≡u2. We extend this uniqueness result to a general class of equations of Benjamin-Ono ...
-
Evolution of Polygonal Lines by the Binormal Flow
(2020-02-05)The aim of this paper is threefold. First we display solutions of the cubic nonlinear Schr ̈odinger equation on R in link with initial data a sum of Dirac masses. Secondly we show a Talbot effect for the same equation. ...
-
A Hardy-type inequality and some spectral characterizations for the Dirac–Coulomb operator
(2020-01-01)We prove a sharp Hardy-type inequality for the Dirac operator. We exploit this inequality to obtain spectral properties of the Dirac operator perturbed with Hermitian matrix-valued potentials V of Coulomb type: we characterise ...
-
Bilinear identities involving the k-plane transform and Fourier extension operators
(2019-11-30)We prove certain L2pRnq bilinear estimates for Fourier extension operators associ- ated to spheres and hyperboloids under the action of the k-plane transform. As the estimates are L2-based, they follow from bilinear ...
-
Carleman type inequalities for fractional relativistic operators
(2019-09-22)In this paper, we derive Carleman estimates for the fractional relativistic operator. Firstly, we consider changing-sign solutions to the heat equation for such operators. We prove monotonicity inequalities and convexity ...
-
On the Evolution of the Vortex Filament Equation for regular M-polygons with nonzero torsion
(2019-09-03)In this paper, we consider the evolution of the Vortex Filament equa- tion (VFE): Xt = Xs ∧ Xss, taking M-sided regular polygons with nonzero torsion as initial data. Us- ing algebraic techniques, backed by numerical ...
-
Some lower bounds for solutions of Schrodinger evolutions
(2019-08-21)We present some lower bounds for regular solutions of Schr odinger equations with bounded and time dependent complex potentials. Assuming that the solution has some positive mass at time zero within a ball of certain radius, ...
-
On the energy of critical solutions of the binormal flow
(2019-07-20)The binormal flow is a model for the dynamics of a vortex filament in a 3-D inviscid incompressible fluid. The flow is also related with the classical continuous Heisen- berg model in ferromagnetism, and the 1-D cubic Schr ...
-
A Hardy-type inequality and some spectral characterizations for the Dirac-Coulomb operator
(2019-07-02)We prove a sharp Hardy-type inequality for the Dirac operator. We exploit this inequality to obtain spectral properties of the Dirac operator perturbed with Hermitian matrix-valued potentials V of Coulomb type: we characterise ...
-
A Hardy-type inequality and some spectral characterizations for the Dirac–Coulomb operator
(2019-06)We prove a sharp Hardy-type inequality for the Dirac operator. We exploit this inequality to obtain spectral properties of the Dirac operator perturbed with Hermitian matrix-valued potentials $\mathbf V$ of Coulomb type: ...
-
Self-similar dynamics for the modified Korteweg-de Vries equation
(2019-04-09)We prove a local well posedness result for the modified Korteweg-de Vries equa- tion in a critical space designed so that is contains self-similar solutions. As a consequence, we can study the flow of this equation around ...
-
Uniqueness Properties of Solutions to the Benjamin-Ono equation and related models
(2019-01-31)We prove that if u1, u2 are solutions of the Benjamin- Ono equation defined in (x, t) ∈ R × [0, T ] which agree in an open set Ω ⊂ R × [0,T], then u1 ≡ u2. We extend this uniqueness result to a general class of equations ...
-
Bilinear identities involving the $k$-plane transform and Fourier extension operators
(2019)We prove certain $L^2(\mathbb{R}^n)$ bilinear estimates for Fourier extension operators associated to spheres and hyperboloids under the action of the $k$-plane transform. As the estimates are $L^2$-based, they follow from ...
-
On the improvement of the Hardy inequality due to singular magnetic fields
(2018-07-12)We establish magnetic improvements upon the classical Hardy inequality for two specific choices of singular magnetic fields. First, we consider the Aharonov-Bohm field in all dimensions and establish a sharp Hardy-type ...
-
On the improvement of the Hardy inequality due to singular magnetic fields
(2018-07-12)We establish magnetic improvements upon the classical Hardy inequality for two specific choices of singular magnetic fields. First, we consider the Aharonov-Bohm field in all dimensions and establish a sharp Hardy-type ...
-
Asymptotics in Fourier space of self-similar solutions to the modified Korteweg-de Vries equation
(2018-07-06)We give the asymptotics of the Fourier transform of self-similar solutions to the modified Korteweg-de Vries equation, through a fixed point argument in weighted W1,8 around a carefully chosen, two term ansatz. Such knowledge ...
-
Asymptotics in Fourier space of self-similar solutions to the modified Korteweg-de Vries equation
(2018-07-06)We give the asymptotics of the Fourier transform of self-similar solutions to the modified Korteweg-de Vries equation, through a fixed point argument in weighted $W^{1,\infty}$ around a carefully chosen, two term ansatz. ...
-
On the regularity of solutions to the k-generalized korteweg-de vries equation
(2018-07)This work is concerned with special regularity properties of solutions to the k-generalized Korteweg-de Vries equation. In [Comm. Partial Differential Equations 40 (2015), 1336–1364] it was established that if the initial ...
-
On the Relationship between the One-Corner Problem and the $M-$Corner Problem for the Vortex Filament Equation
(2018-06-28)In this paper, we give evidence that the evolution of the vortex filament equation (VFE) for a regular M-corner polygon as initial datum can be explained at infinitesimal times as the superposition of M one-corner initial ...
-
Spectral stability of Schrödinger operators with subordinated complex potentials
(2018-06-28)We prove that the spectrum of Schroedinger operators in three dimensions is purely continuous and coincides with the non-negative semiaxis for all potentials satisfying a form-subordinate smallness condition. By developing ...
-
Absence of eigenvalues of two-dimensional magnetic Schroedinger operators
(2018-01-01)By developing the method of multipliers, we establish sufficient conditions on the electric potential and magnetic field which guarantee that the corresponding two-dimensional Schroedinger operator possesses no point ...
-
On the regularity of solutions to the k-generalized korteweg-de vries equation
(2018-01-01)This work is concerned with special regularity properties of solutions to the k-generalized Korteweg-de Vries equation. In [Comm. Partial Differential Equations 40 (2015), 1336–1364] it was established that if the initial ...
-
Absence of eigenvalues of two-dimensional magnetic Schr ̈odinger operators
(2017-10-17)By developing the method of multipliers, we establish sufficient conditions on the electric potential and magnetic field which guarantee that the corresponding two-dimensional Schr ̈odinger operator possesses no point ...
-
Uniqueness properties for discrete equations and Carleman estimates
(2017-03-25)Using Carleman estimates, we give a lower bound for solutions to the discrete Schrödinger equation in both dynamic and stationary settings that allows us to prove uniqueness results, under some assumptions on the decay of ...
-
Singularity formation for the 1-D cubic NLS and the Schrödinger map on $\mathbb{S}^2$
(2017-02-02)In this note we consider the 1-D cubic Schrödinger equation with data given as small perturbations of a Dirac-$\delta$ function and some other related equations. We first recall that although the problem for this type of ...
-
A strategy for self-adjointness of Dirac operators: Applications to the MIT bag model and delta-shell interactions
(2016-12-21)We develop an approach to prove self-adjointness of Dirac operators with boundary or transmission conditions at a $C^2$-compact surface without boundary. To do so we are lead to study the layer potential induced by the ...
-
Hardy uncertainty principle, convexity and parabolic evolutions
(2016-09-01)We give a new proof of the $L^2$ version of Hardy’s uncertainty principle based on calculus and on its dynamical version for the heat equation. The reasonings rely on new log-convexity properties and the derivation of ...
-
An Isoperimetric-Type Inequality for Electrostatic Shell Interactions for Dirac Operators
(2016-06-01)In this article we investigate spectral properties of the coupling $H + V_{\lambda}$, where $H =-i\alpha \cdot \nabla + m\beta$ is the free Dirac operator in $\mathbb{R}^3$, $m>0$ and $V_{\lambda}$ is an electrostatic shell ...
-
The initial value problem for the binormal flow with rough data
(2015-12-31)In this article we consider the initial value problem of the binormal flow with initial data given by curves that are regular except at one point where they have a corner. We prove that under suitable conditions on the ...
-
Shell interactions for Dirac operators: On the point spectrum and the confinement
(2015-12-31)Spectral properties and the confinement phenomenon for the coupling $H + V$ are studied, where $H =-i\alpha \cdot \nabla + m\beta$ is the free Dirac operator in $\mathbb{R}^3$ and $V$ is a measure-valued potential. The ...
-
Erratum to: Relativistic Hardy Inequalities in Magnetic Fields [J Stat Phys, 154, (2014), 866-876, DOI 10.1007/s10955-014-0915-0]
(2015-12-31)[No abstract available]
-
The Vortex Filament Equation as a Pseudorandom Generator
(2015-08-01)In this paper, we consider the evolution of the so-called vortex filament equation (VFE), $$ X_t = X_s \wedge X_{ss},$$ taking a planar regular polygon of M sides as initial datum. We study VFE from a completely novel ...
-
The dynamics of vortex filaments with corners
(2015-07-01)This paper focuses on surveying some recent results obtained by the author together with V. Banica on the evolution of a vortex filament with one corner according to the so-called binormal flow. The case of a regular polygon ...
-
Vortex filament equation for a regular polygon
(2014-12-31)In this paper, we study the evolution of the vortex filament equation,$$ X_t = X_s \wedge X_{ss},$$with $X(s, 0)$ being a regular planar polygon. Using algebraic techniques, supported by full numerical simulations, we give ...
-
Relativistic Hardy Inequalities in Magnetic Fields
(2014-12-31)We deal with Dirac operators with external homogeneous magnetic fields. Hardy-type inequalities related to these operators are investigated: for a suitable class of transversal magnetic fields, we prove a Hardy inequality ...
- CEX2021001142-S acredited as "Centro de Excelencia Severo Ochoa". MINECO, Spain. 01/01/2023 - 31/12/2026. Total amount: 4.000.000€
- SEV-2017-0718 acredited as "Centro de Excelencia Severo Ochoa". MINECO, Spain. 01/07/2018 - 30/06/2022. Total amount: 4.000.000€
- IT-1247-19 Análisis matemático y numérico de algunas ecuaciones en derivadas parciales y sus aplicaciones. Basque Government, Spain. 01/01/2019 - 31/12/2021. Total amount: 326.500€
- PGC2018-094522-B-I00, Análisis matemático y numérico de algunas ecuaciones en derivadas parciales y sus aplicaciones. Ministry of Science and Innovation, Spain.01/01/2019 - 31/12/2021. Total amount: 125.780€
- 669689-HADE-Harmonic Analysis and Differential Equations: new challenges. ERC-EA European Research Council Executive Agency (H2020). 01/12/2015-30/11/2021. Total amount: 1.672.103€
- SEV-2013-0323 accredited as "Centro de de Excelencia Severo Ochoa-Severo Ochoa Excellence Center". MINECO, Spain 01/07/2014-30/06/2018. Total amount: 4.000.000€
- IT-641-13 Mathematical Physics, mathematical Analysis and PDEs and Numerical Analysis. Basque Government, Spain. 01/01/2013-31/12/2018. Total amount: 302.000€
- MTM2014-53145-P Analisis teórico y numérico de ecuaciones de evolución. MINECO, Spain 01/01/2015-31/12-2017. Total amount: 102.000€
- BERC.2014-2017 Centros de Investigación Básica y de Excelencia. Basque Government 01/01/2014-01/12/2017
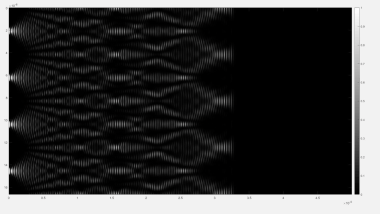
Numerical study of the time evolution of the Talbot effect for infinite periodic diffraction grating
This video shows the propagation of the intensity of a plane wave after travelling through an infinite and periodic diffraction grating. The simulation is done using a finite elements method. It's aim is to show the time evolution and shaping of the Talbot effect.
News
- (ES) El Análisis de Fourier y las Ecuaciones Diferenciales, Nuevos Retos - 2021-04-28
- (EN) Fourier Analysis and Differential Equations, New Challenges - 2021-04-28
Dissemination activities
| Date | Title | Place |
|---|---|---|
| 2023-06-16 | Desingularization of the Biot-Savart integral and the Localised Induction Approximation (LIA) | Bilbao |
| 2023-05-24 | Blow-up for the 1d cubic NLS and related systems | IHES, Conference in honor of F-Merles. Bures sure Yvette, France |
| 2023-03-13 | New Conservations Laws and Energy Cascade for 1d Cubic NLS | University of Cambridge, Depart. of Mathematics |
| 2022-03-17 | Matemáticas y Turbulencia | Universidad Politécnica de Madrid |
| 2022-08-08 | Intermittency and the Talbot effect | Université Lyon |
| 2021-11-01 | Lower Bounds fro Oscilatory Integrals | Depart. of Mathematics, Brown University, RI, USA |
| 2021-10-18 | Fluctuations of ∂-moments free Schrödinger equation | ICERM, Brown University, RI, USA |
| 2021-09-17 | Riemmann's non-differentable function and the binormal curvature flow | ICERM, Brown University, RI, USA |
| 2021-08-02 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - Inst. Matem Pura e Appl (IMPA), Rio de Janeiro, Brasil |
| 2021-05-05 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - Ecole Normale Superieure de Lyon |
| 2021-04-12 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - Math. Science Res Int. (MSRI), Berkeley, USA |
| 2021-01-08 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - NYU Abu Dhabi |
| 2020-12-08 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - One World PDE Seminar, Portugal |
| 2020-10-28 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - Fields Institute, Toronto |
| 2020-10-24 | Riemmann's non-differentable function and the binormal curvature flow | Toronto |
| 2020-10-20 | Riemmann's non-differentable function and the binormal curvature flow | Virtual - Building Bridges - Academia Europea Barcelona Knowledge Hub |
| 2020-09-10 | The binormal flow, the Talbot effect, and non-circular jets | PDE Zoom-seminar, Shanghai |
| 2019-02-08 | Lower bounds for Schrödinger evolutions | UCSB |
| 2017-01-27 | Shell interactions for dirac operators. an isoperimetric-type Inequality | Zaragoza |
| 2016-12-14 | Singular solutions of the Binormal Flow: transfer of energy and momentum | Valdivia, Chile |
| 2016-10-20 | The Talbot Effect and The Ecolution of Vortex Filaments | MSRI, USA |
| 2016-08-23 | Shell interactions for Dirac operators: An isoperimetric-type inequality | Sapporo, Japan |
| 2016-05-09 | Las matemáticas en la hora de la innovación | Periódico "El Correo" |
| 2015-06-25 | Some Remarks about the Uncertainty Principle | UAM, Spain |
| 2015-06-17 | The Vortex filament equation for a regular polygon and the Talbot effect | https://www.youtube.com/watch?v=Z1gXJKLw2Fo |
| 2014-11-13 | El tablero de Galton | Facultad de Ciencia y Tecnología de la UPV/EHU |
| 2014-09-21 | Shell interactions for Dirac operators: selfadjointeness, point spectrum, and confinement | Chicago, USA |
| 2012-11-02 | Las matemáticas están para usarlas | UPV/EHU, Spain |
| 2011-10-19 | Asymptotic Lower Bounds for Solutions to Dispersive Equations | Mexico DF |
| 2011-09-01 | A New Approach to Hardy's Uncertainty Principle | Lexington |
| 2011-06-14 | Unidad de Biomedicina Cuantitativa | BioCruces, Barakaldo |
| 2011-06-10 | A Geometric Description of the Formation of Singularities in the Binormal Flow | ETH Zurich |
| 2011-02-01 | ¿Matemáticas? Sí, gracias. | Periódico "El Correo" |
| 2010-06-01 | Oscilatory Integrals and Euler Equations | CSIC Madrid |
| 2006-01-03 | The initial value problem for non-linear Shrödinger equations | ICM Madrid |
- Ministry of Science and Technology, Spain - PI of the Strategic Network of Mathematics - Scientific Committee 2020
- International Congress of Industrial and Applied Mathematics (ICIAM) - Officer - Scientific Committees - October 2019 - December 2019
- European Academy of Sciences, Division of Mathematics - Officer - Scientific Committee - March 2019 - March 2023
- Journal Serie A Matemáticas, Spanish Academy of Sciences - General Editor - 2018
- L'institut Universitaire de France (IUF) - Member of the Comission - Scientific Committees - 2016-2017
- Asociación ICIAM Valencia 2019 - Vice-presicent - Scientific Committees - 2014-2019
- Basque Center for Applied Mathematics (BCAM) - Scientific Director - Scientific Committee 2013-2019
- Spanish Candidacy for ICIAM Valencia 2019 - Defensor of the bid - Scientific Committee - 2013
- Journal Serie A Matemáticas, Spanish Academy of Sciences - Member of the Editorial Boards - 2013
- Training and Research Unit of Mathematics and Applications (UPV/EHU) - Director - Scientific Committee - 2012-2013
- Spanish Candidacy for ICIAM Valencia 2019 - Defensor of the prebid - Scientific Committee - 2012
- Mathematical European Week-end, Bilbao - Chair of the Program Committee - Scientific Committee - 2011
- Linköping University, Sweden - Jury Member - Scientific Committee - 2011
- Department of Quantitative Biomedicine, Biocruces Research Institute - Director - Scientific Committee - 2011
- Academy of Finland - Panel member of the research projects - Scientific Committee - 2010
- Spanish Royal Mathematical Society (RSME) - Vice-president - Scientific Committee - 2009-2012
- ICIAM - Member of the Executive Board - Scientific Committee - 2008-2013
- University of the Basque Country/Universidad del País Vasco/Euskal Herriko Unibertsitatea (UPV/EHU) - Director of the PhD Programme in Mathematics - Scientific Committee - 2007 - 2013
- Inter-university master program in Applied Mathematics (UPV/EHU and another four universities) - Director - Scientific Activities - 2006-2012
- Habilitation and PhD theses at several foreign universities - Jury Member - Scientific Committee - 2004
- Medalla Real Sociedad Matemática Española (RSME) 2023 - Spanish Royal Mathematical Society (RSME) Medal 2023, Spain, 2023
- Severo Ochoa Excellence Accreditation, BCAM, 2023-2026
- National Research Award "Julio Rey Pastor" 2021, in Mathematics and Information and Communication Technologies
- Severo Ochoa Excellence Accreditation, BCAM, 2018-2022
- Severo Ochoa Excellence Accreditation, BCAM, 2014-2018
- ERC-Advance Grant, European Research Council, Brussels, Belgium, 2015-2021
- Elected member of the Real Academia de Ciencias, Spain, 2018
- Member of the European Academy of Sciences; European Academy of Sciences, Liege, Belgium, 2014
- Blaise Pascal Medal, European Academy of Sciences, Liege, Belgium, 2014
- Le Prix La Recherche, Mathematiques, France, 2014
- Member of the "Real Academia de Ciencias Exactas, Físicas y Naturales-RAC", Spain, 2013
- Fellow of the American Mathematical Society, Inaugural Class, 2012
- Premio Euskadi de Investigación - Euskadi Research Prize, Basque Government, Spain, 2012
- Highly Cited Researcher, ISI Web os Science, 2004
- Iberdrola grant for Visiting Fellows, Spain, 1997
- National Science Foundation grant, USA, 1989-90

 ;
; 